作者:九号线
题图:九号线微信公众号
《川总写量化》前几天写了一篇公众号《Farewell,ad-hoc 多因子模型》,指出了传统ad-hoc多因子模型在资产定价方面面临的挑战,并指出“最近几年实证资产定价的研究范式已从ad-hoc多因子模型转到隐性多因子模型,其中代表作当属基于PCA方法的Kelly, Pruitt, and Su (2019) 以及 Kozak, Nagel, and Santosh (2020)。
择日不如撞日,今天我们就来重点介绍一下Kelly,Pruitt,and Su (2019)的这篇2019年JFE BEST PAPER——《Characteristics Are Covariances :A Unified Model of Risk and Return》,这篇论文基于隐因子和动态载荷模型,提出了一个统一的资产定价框架。内容略有点枯燥,但读完后一定会有收货。
一、IPCA原理简介
首先作者提出了一个改进版的PCA——IPCA,即Instrumented Principal Component Analysis。
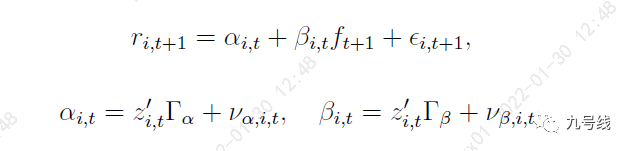
这里r_i,t+1 是股票或资产i在t+1时刻的收益率,a_i,t是截距项,即承担风险暴露也无法解释的“anomalous return”,β_i,t和f_t+1分别是因子风险暴露和因子收益率。值得注意的是,区别于传统PCA方法,这里的a_i,t、β_i,t都是随时间动态变化的,这也是作者把这个模型称之为条件资产定价模型,传统的模型(如我们熟知的CAPM、FF3、FF4、FF5等)则称之为静态或无条件资产定价模型。
进一步的,a_i,t、β_i,t又分别和资产的特征向量z_i,t(characteristics)以及参数矩阵Γ_a和Γ_β有关。这里作几点说明:
1、资产的特征z_i,t和因子是不同的概念,举例来说,某股票的pe、pb、ps、peg属于不同特征,但他们都属于估值因子范畴;
2、由下标可以发现,z_i,t是随资产类别i和时间t不断变化的,而Γ_a和Γ_β是全局固定不变的,即所有资产在所有时间序列上共享一个Γ_a和Γ_β。
整个模型的待估计参数主要是隐因子f_t+1和参数矩阵Γ_a、Γ_β。根据结局项a_i,t是否为0,整个模型又可以分为限制型(Γ_a=0)和非限制型(Γ_a not =0),当然两个模型可以统一表述为如下模型:
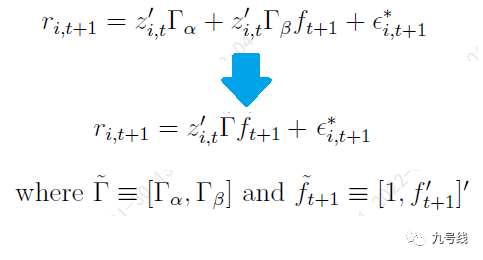
作者采用交替最小二乘法(Alternating Least Squares)对上式进行优化求解,有点类似EM算法,即先固定f_t+1优化求解Γ_a、Γ_β,然后在固定Γ_a、Γ_β优化求解f_t+1,直到模型收敛,

这里f_t+1的估算其实就是回归方程的显性解,矩阵Γ_a、Γ_β的估算用到了克罗内科积。注意这里为了计算方便,先优化求解Γ_a、Γ_β的向量形式vec(Γ_a、Γ_β),然后在转换成矩阵形式。此外,为了便于和传统PCA比较,作者根据每个股票特征构建了基于特征的组合:
此处x_t+1的元素l代表t+1时刻,根据每个股票的特征l加权构建的组合收益率

经过层层迭代后得到上式,其实就是主成分求解半正定举证前K大特征向量的形式。具体推导过程不再赘述,有兴趣的朋友可以参考Kelly,Pruitt,and Su的《Instrumented Principal Component Analysis》。像我一样偷懒的朋友也可以直接去作者网站下载源代码,python版本和matlab版本都有:https://sethpruitt.net/2020/06/28/instrumented-principal-component-analysis/。
接下来作者运用上述IPCA方法,对资产定价模型做了3方面检验:
1、检验截距项a_i,t可否显著为0;
2、检验IPCA模型相较于传统因子模型(CAPM、FF3、FF4、FF5、FF6)优势;
3、检验资产特征对整个模型的贡献度;
对于模型整体拟合效果的检验,作者分别采用Total R^2和Predictive R^2,前者采用估计的因子收益f_hat_t+1,后者采用因子的条件预期收益率λ_hat(conditional expected returns)。
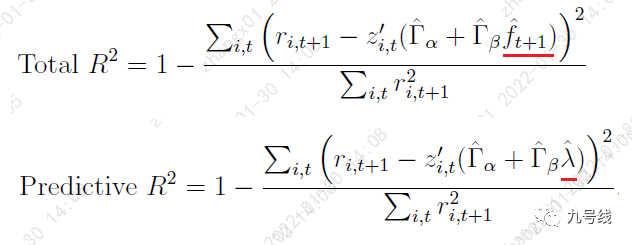
对于截距项a_i,t可否显著为0、IPCA模型加入传统显性因子后的边际改善效果以及单个特征对模型的边际改善效果的检验,作者采用基于bootstrap的类沃尔德检验(Wald-type test statistic)。
二、数据说明
1、采用1962/1~2014/5期间共12813家上市公司的月频数据作为研究对象;
2、选取包括动量、市值、杠杆率、换手率、投资比例、估值等常见指标在内的共36个特征,并分别取均值和均值偏差作为输入特征,同时添加一个常数项1,所以最终每个股票的特征向量为:
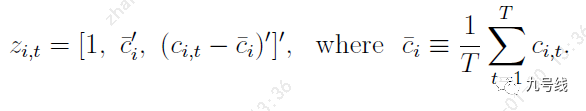
3、为了兼顾不同特征的不同量纲,首先对每个股票的每个特征进行时间序列标准化处理(减去均值/标准差),然后每个截面t对所有股票的某一特征进行(排序标准化 - 0.5),最终每个股票的特征取值范围为[-0.5,0.5]。
三、实证检验结果
1、截距项a_i,t可否显著为0?
当K>1时,截距项a_i,t未通过Wald tets,即无法拒绝a_i,t=0的假设。
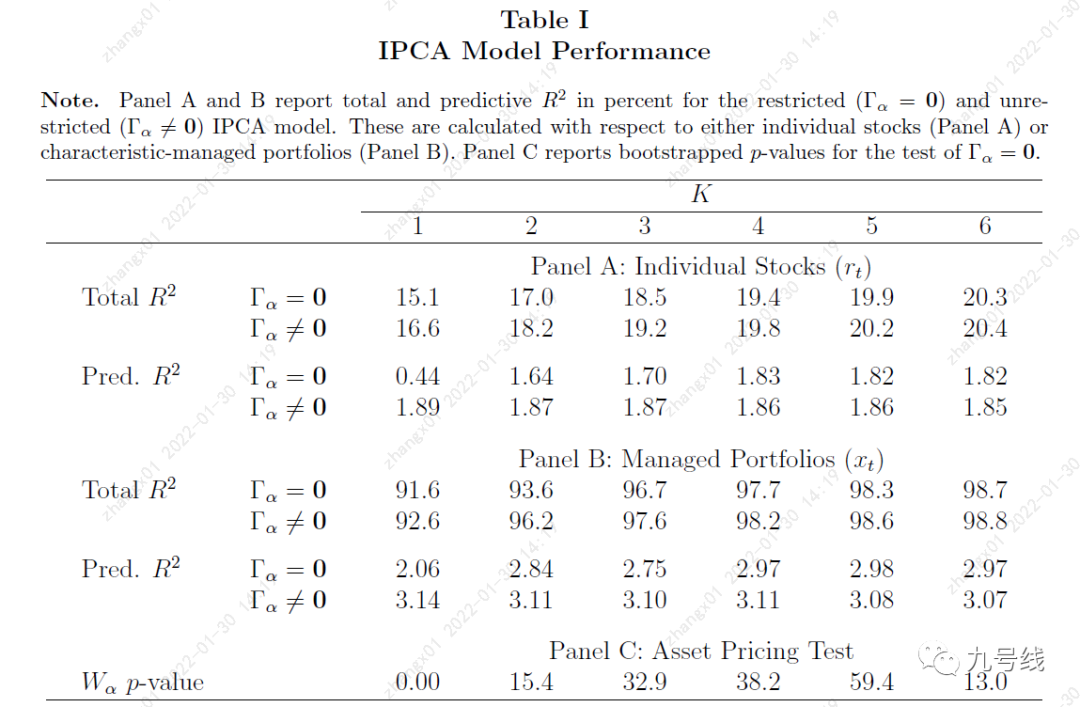
从另一个维度来验证,相较于传统因子模型(比如下图中的FFC6,即FF5+动量),IPCA(取K=4)无论是静态模型(Unconditional,假设风险暴露不变即β_i,t=β_i)还是时变模型(conditional),剥离后的alpha几乎为0且不显著。
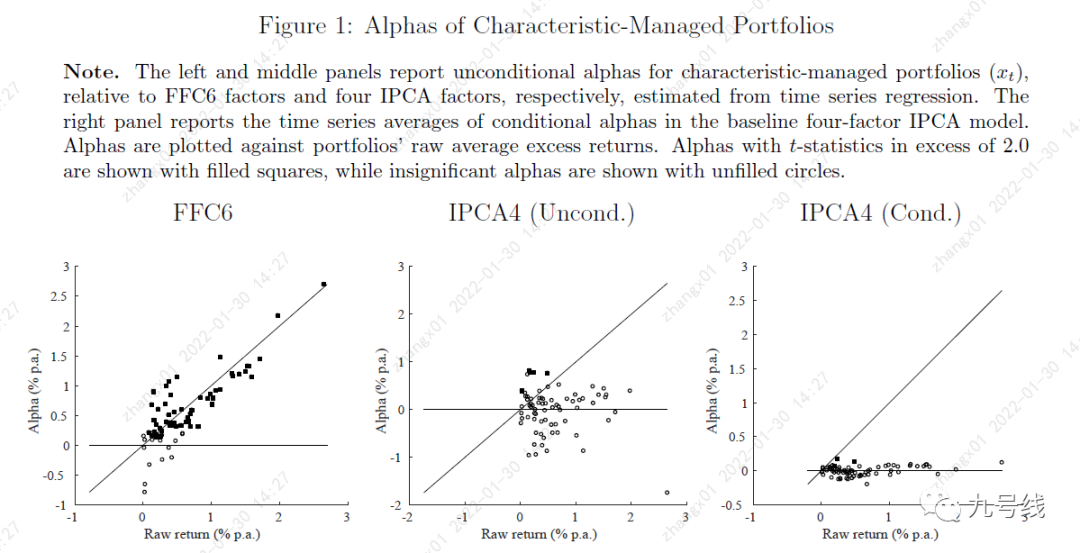
也就是说,采用IPCA定价模型且随着隐因子数量增加,股票截面收益可以完全由特征映射的风险暴露Γ_β和风险因子f_t+1解释,而不需要截距项“anomalous return”来解释。
2、IPCA模型相较于传统因子模型(CAPM、FF3、FF4、FF5、FF6)优势
下图PanelA即本文提出的IPCA定价模型,PanelB的1、3、4、5、6列分别对应传统CAMP、FF3、FF4、FF5、FF6因子模型,PanelC分别是上述传统因子模型叠加动态风险暴露,PanelD是传统主成分分析法。
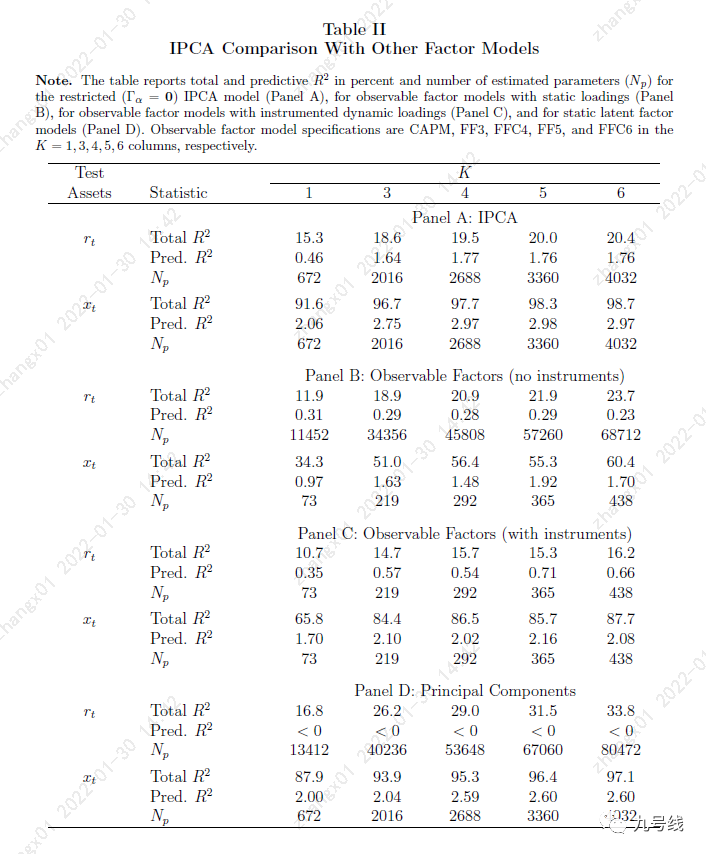
上图可以看出,无论是针对个股检验还是特征组合检验,IPCA定价模型的Total R^2和Predictive R^2均要优于传统因子模型。而当传统因子模型采用动态风险载荷后,虽然Total R^2有所降低,但Predictive R^2显著提高。值得注意的是:当运用传统主成分分析对个股资产定价时,虽然Total R^2优于IPCA,但Predictive R^2均为负,对基于预期收益的解释效果非常差。
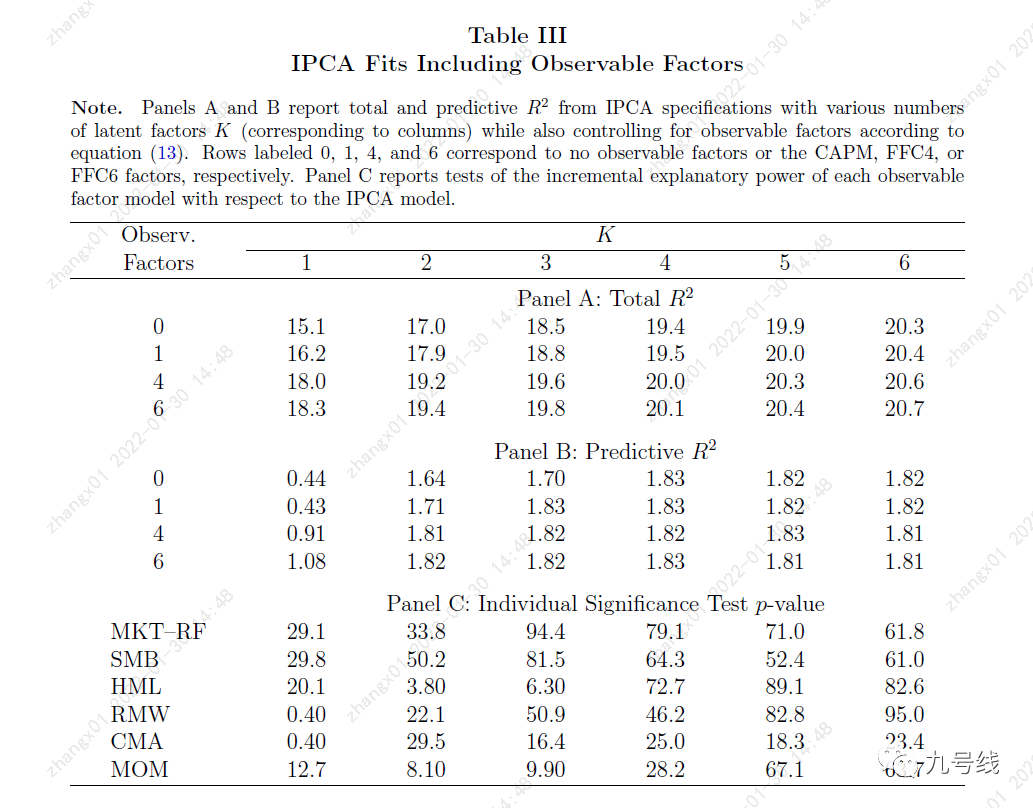
进一步,作者在IPCA基础上逐步加入传统因子。从下图可以看到,当隐因子K=1时,加入显性因子模型可以将定价模型的Total R^2从15.1%提高至18.3%、Predictive R^2从0.44%提高至1.08%,其中使模型得到显著改善的两个因子是RMW和CMA。
然而,随着隐因子K的增加,IPCA加入传统因子对模型的改善效果大幅减弱,甚至当K=5时,加入FF6因子后模型的Predictive R^2反而下降。
这也从侧面反映,随着隐因子K的增加,IPCA模型能够提取绝大多数对资产定价有影响的风险因子。
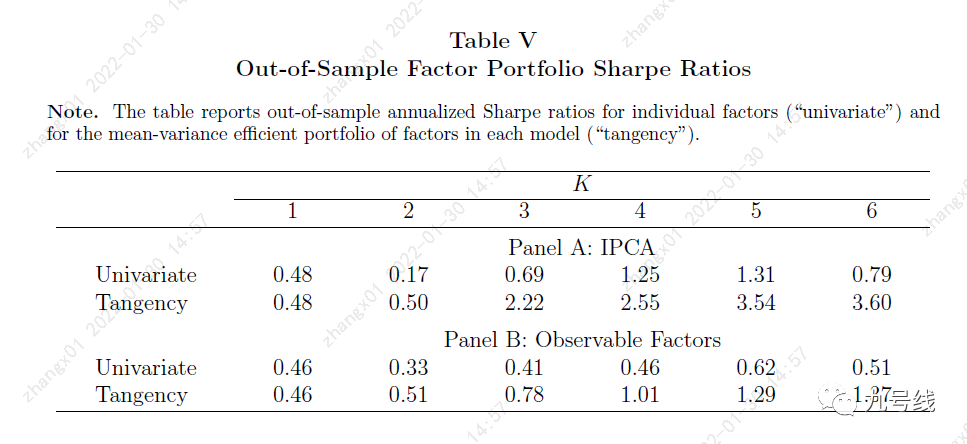
另一方面,作者基于IPCA隐因子和传统显性因子,通过均值方差模型构建最优sharp组合(Factor Tangency Portfolios)。发现随着因子数量的增加,基于隐因子构建的最优组合相较于传统因子构建的最优组合,有更高的SharpRatio。
这似乎说明, IPCA能够更好的捕捉到资产特征背后隐含的extensive co-movement,从而为因子投资提供了一个新的研究方向。
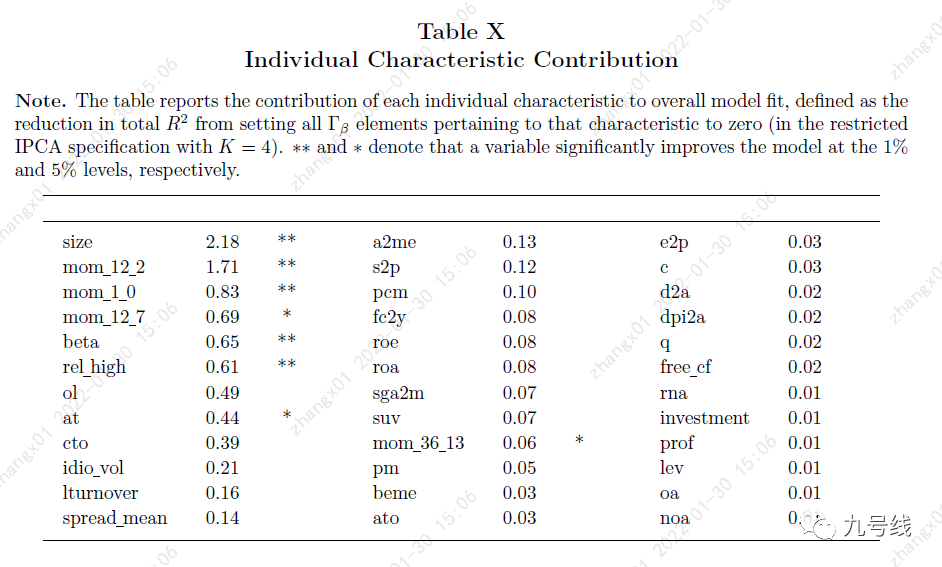
3、检验资产特征对整个模型的贡献度
最后 ,作者对所有73个特征(实际只有36个)的边际贡献进行验证,发现真正起到核心定价作用的主要是size、动量、beta、relative high price (rel high)、total assets(log at)等8个特征。
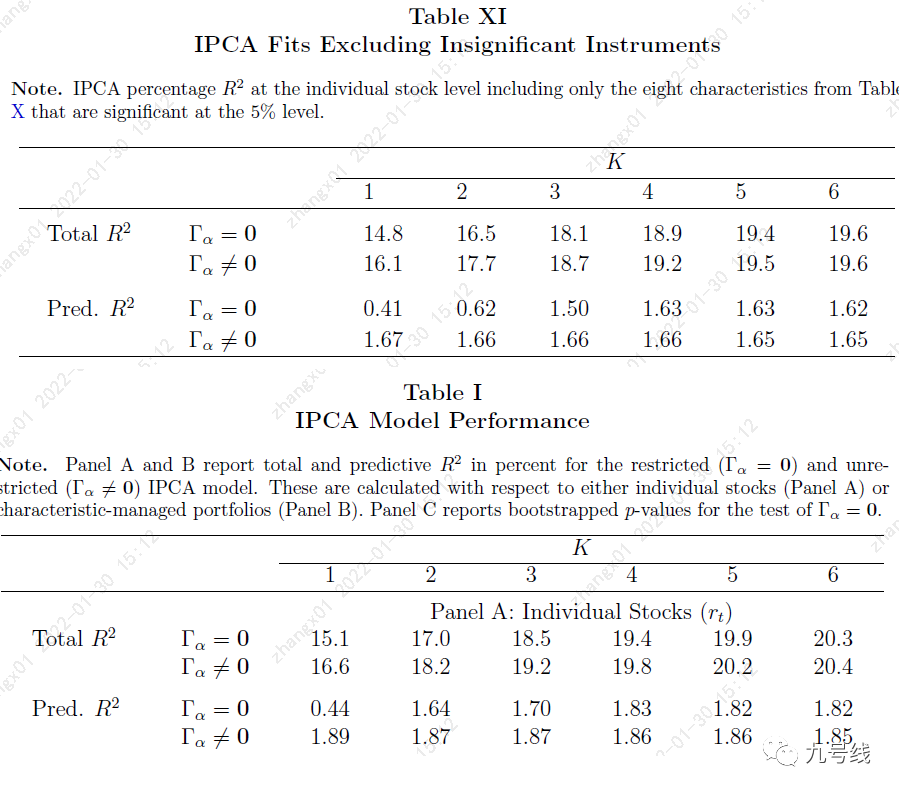
于是,作者仅使用size、动量、beta、relative high price (rel high)、total assets(log at)这8个特征构建IPCA模型对所有股票进行定价,并跟之前使用73个特征的模型对比(即上面Table1的PanelA,为了方便比较我再次复制到下面),发现两个模型的Total R^2和Predictive R^2几乎差不多。这就说明,仅部分特征对股票截面收益率的定价起决定性作用,绝大部分特征可以忽略。
鲁棒性检验部分,作者又分别将全部股票划分为large和small两个子样本,即大市值、小市值股票,同时运用年度频率的特征和收益率,使用IPCA对股票进行定价,得到了类似的结论,说明基于IPCA方法的资产定价模型有较好的稳定性。
至此,一个基于隐因子、动态载荷的资产统一定价模型初具雏形,无论从结果还是背后的经济学逻辑,似乎都优于传统因子定价模型。当然,这并不能说传统多因子模型已经过时了,不同学派之间的斗争未来一定会愈演愈烈,只能感慨学术圈太卷了。。。。。
四、参考文献
1、Bryan Kelly、Seth Pruitt、Yinan Su:《Instrumented Principal Component Analysis》
2、Bryan Kelly、Seth Pruitt、Yinan Su:《Characteristics Are Covariances :A Unified Model of Risk and Return》
3、Bryan Kelly、Seth Pruitt、Tobias Moskowitz:《Understanding Momentum and Reversal?》
版权声明:文章版权归原作者所有,部分文章由作者授权本平台发布,若有其他不妥之处的可与小编联系。
