一文梳理热门神经网络时序预测模型

作者：九号线

题图：九号线微信公众号

先插个题外话，前段时间知名学术论文审稿平台 OpenReview上，一个前端 bug 导致数据库泄露，让原本的双盲评审变成了明牌——大家可以看到每篇论文的审稿人以及每个人的打分情况。尤其是那些低分论文，打低分的理由各不相同，有些确实不认可论文创新思路，有些是纯粹是个人恩怨了，更可恶的是通过打低分从而给自己正在写的同赛道论文「让路」,学术圈的江湖恩怨由此公布与众。

扯远了，回到正题。时序预测（TSF）一直是学术界热门研究方向，尤其在金融投资领域，如经济数据预测、资产收益率/波动率预测、资产相关性预测等等许多方面都会涉及单变量/多变量时序预测。近几年，随着深度学习技术尤其是基于多层感知器（MLP）、循环神经网络（RNN）、卷积神经网络（CNN）、Transformer等模型的提出，极大地推动了时序预测的发展。这点可以从每年在NIPs、ICLR等人工智能顶会上大量发布的相关论文即可证明，这些论文从不同维度（如对初始序列分解、魔改基座模型内部结构、不同基座模型排列组合等）提出思路创新以提高时序预测的预测效果。

比如之前在《基于二维神经网络模型的一维时序预测——TimesNet系列》一文中，曾简单介绍过TimesNet和MSGNet两个模型及其在时间序列预测的应用效果，最近花了点时间深入研究后，打算系统性地梳理总结一下该领域近些年新发布的热门SOTA模型。总的来说，根据所采用的基座模型对当前各种神经网络时序预测模型进行分类，可大致分为如下几类：

0、基于RNN：比如LSTM、GRU及其各种变形；

1、基于MLP：TiDE（Das 等，2023）、DLinear/NLinear（Zeng等，2023）、TimeMixer（Wang 等，2024）；

2、基于Transformer：InFormer（Zhou等，2021）、FedFormer（Zhou等，2022）、PatchTST（Nie 等，2023）、CrossFormer（Zhang等，2023）、iTransformer（Liu 等，2024）；

3、基于CNN：TimesNet（Wu 等，2023）、 MICN（Wang 等，2023）；

4、基于GCN：MSGNet（Cai 等，2024）；

5、多模型结合：PDF（Dai 等，2024，Transformer+CNN）、TimeMixer++（Wang 等，2025，CNN+Attention）

RNN模型如LSTM、GRU等这里就不介绍了，单独的RNN模型在主流时序预测任务上的效果都很一般，远远落后于近些年新冒出的各种模型。所以下文重点介绍后面几大类，尤其是最近一两年（2023年以来）发布的SOTA模型

一、基于线性模型（MLP）的时序预测模型

1、TiDE

谷歌研究团队于2023年发表的论文《Long-term Forecasting with TiDE: Time-series Dense Encoder》提出了TiDE（Time-series Dense Encoder）模型。

TiDE是一个基于多层感知机（MLP）的线性模型，采用编码器-解码器架构，旨在简化长期时间序列预测。该模型结合了线性模型的简单性和速度，同时能够有效处理协变量以及非线性依赖。模型整体构架如下：

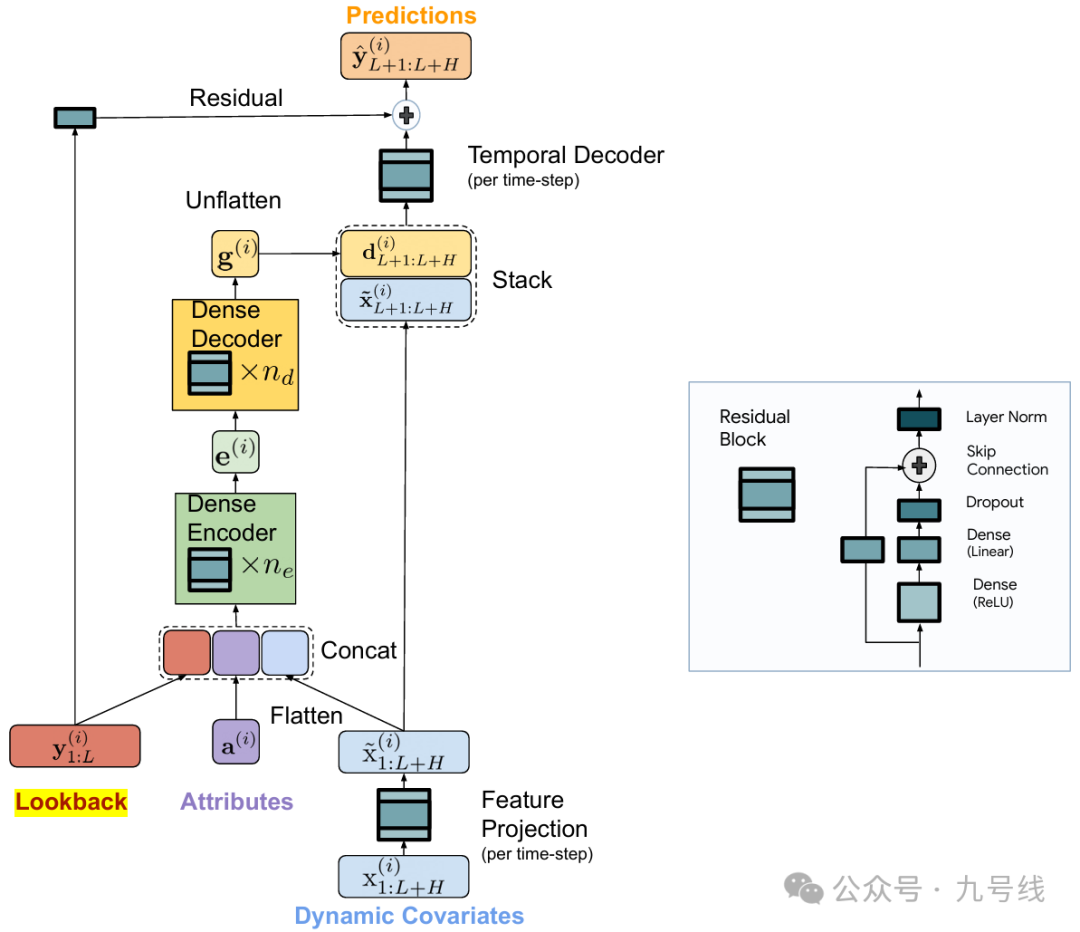
TiDE网络由以下几个关键组成部分：

（1）n_e层的DenseEncoder：TiDE使用密集MLP来编码时间序列的过去信息以及协变量；

（2）n_d层的DenseDecoder：解码器同样基于密集MLP，用于处理编码后的时间序列和含未来信息的协变量，下面会解释为啥包含未来信息；

（3）TemporalDecoder：最终的预测是通过每个时间步的解码向量与该时间步的投影特征来形成的，然后将所有时间步拼接；

（4）全局线性残差连接：从回溯到预测范围，模型还增加了一个全局线性残差连接。

由于TiDE是一个单通道（即每次输入一个变量）预测模型，所以没有考虑变量间的相互影响，但引入了协变量x概念。模型有三个输入：协变量序列x_1:L+H、时间序列y_1:L以及静态影响因素a。这里L是回看步长、H是预测步长。

协变量x是影响时间序列y的一些外部动态因素，比如对于交通数据来说，x可能是星期因素或者节假日因素等，所以预测y_L:L+H的时候，x_L:L+H是实现知道的。这一点对于预测宏观经济数据来说是有用的，因为经济数据存在节假日效应。而静态影响因素a是不随时间变化的影响因素，可以理解为截距项。

此外协变量序列x_1:L+H要先做一次特征映射（Feature Projection），目的是把高维x向量（如果影响因素非常多的话）降维至低维，然后再和y_1:L、a做一次拼接后输入DenseEncoder。

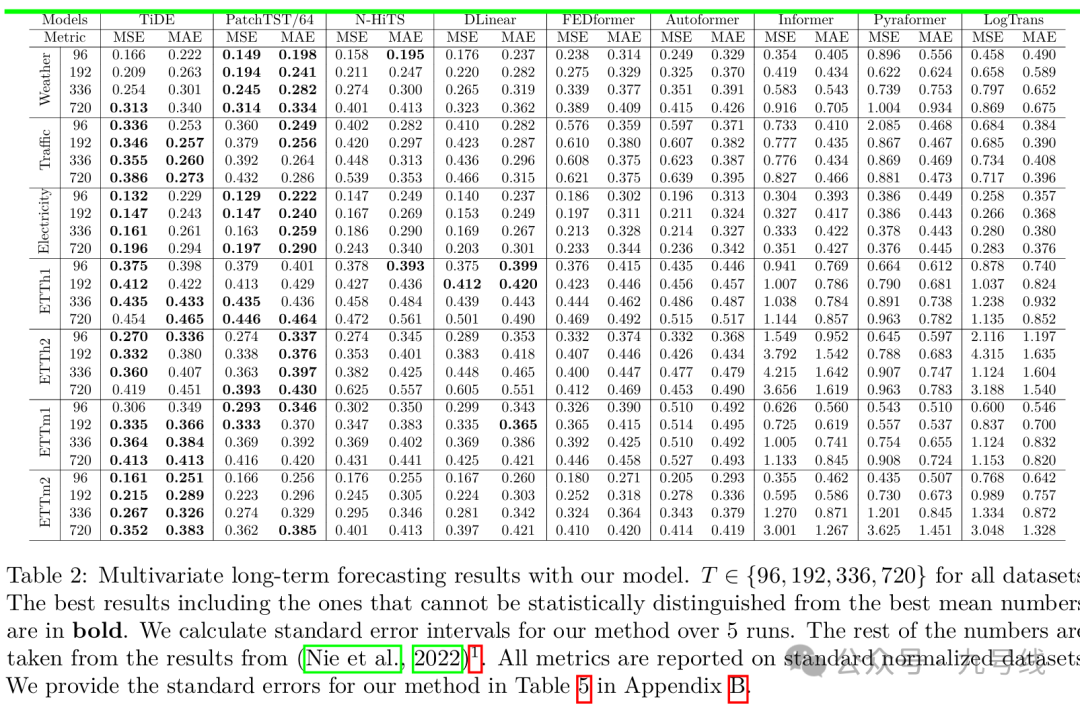
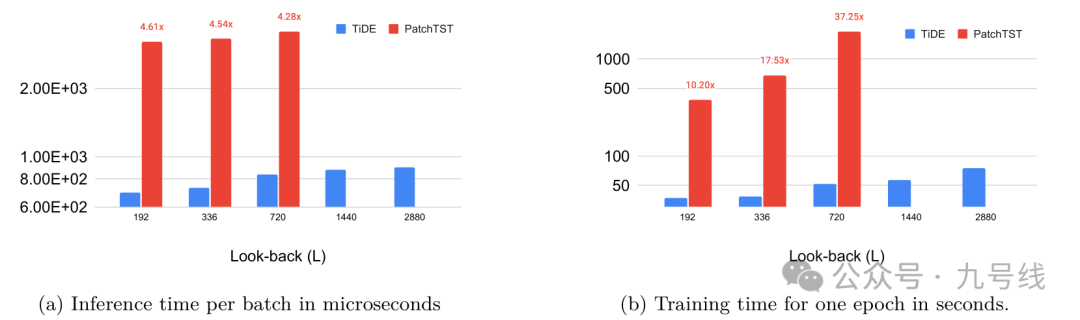
虽然只是线性模型的叠加，TiDE在大部分任务上的预测效果均优于Transformer类模型。尽管部分任务上的预测效果不如PatchTST，但相比PatchTST花费更少的单位epoch训练时间。

2、DLinear/NLinear

同样是2023年，来自香港中文大学的论文《Are Transformers Effective for Time Series Forecasting?》提出了对过往基于Transformer模型的质疑，并提出了一个非常简单的线性模型LTSF-Linear（DLinear/NLinear）用来作为“挑战者”进行对比。

文章作者首先认为那些Transformer类模型的对比实验中所使用的非 Transformer基线方法，基本都是采用自回归（比如ARIMA）或迭代式多步预测（IMS），即要预测T+L时刻先要预测T+L-1时刻，而这些传统方法在 LTSF 任务中容易出现严重的误差累积问题。因此，作者采用直接多步预测（Direct Multi-Step，DMS）策略来挑战现有的Transformer类模型。

模型的构架很简单，作者甚至只用了一张图来说明其理念，看了下源代码就是MPL层的堆叠，而且模型没有考虑不同变量间的相关性。

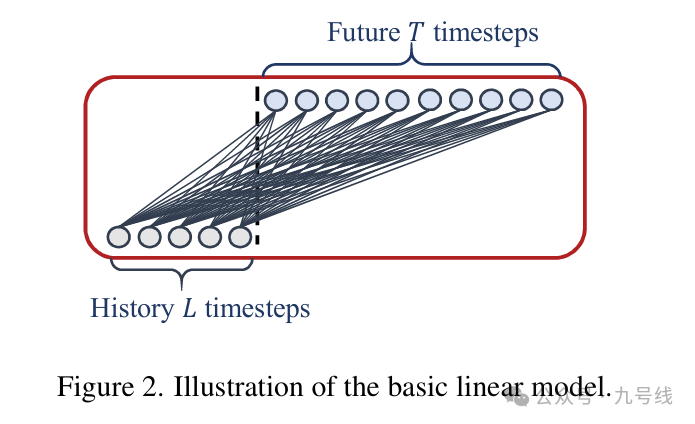
LTSF-Linear包含两个模型：DLinear和NLinear

DLinear：使用移动平均核将原始输入数据分解为趋势成分和残差（季节性）成分，然后分别对这两部分分别使用线性层提取特征，最后将两部分特征相加，得到最终预测结果。在存在明显趋势的数据中，这种方式能增强模型的性能。

NLinear：NLinear先将原始输入序列减去最后一个时间步的值，然后将处理后的数据输入线性层，然后再加回被减去的部分并作最终预测。这种减法和加法可以看作是对输入序列的一种简单归一化，提升了模型的泛化能力。

在9个常用数据集上的实验得到了令人惊讶的结果，在多变量预测任务中，LTSF-Linear 的性能在多数情况下都优于Transformer类模型，哪怕是当时最先进的FEDformer，提升幅度达到 20% ~ 50%，而它甚至还没有建模变量之间的相关性。在不同类型的时间序列任务中，NLinear 和 DLinear 分别展现出更强的应对数据分布偏移和趋势-季节性模式的能力。

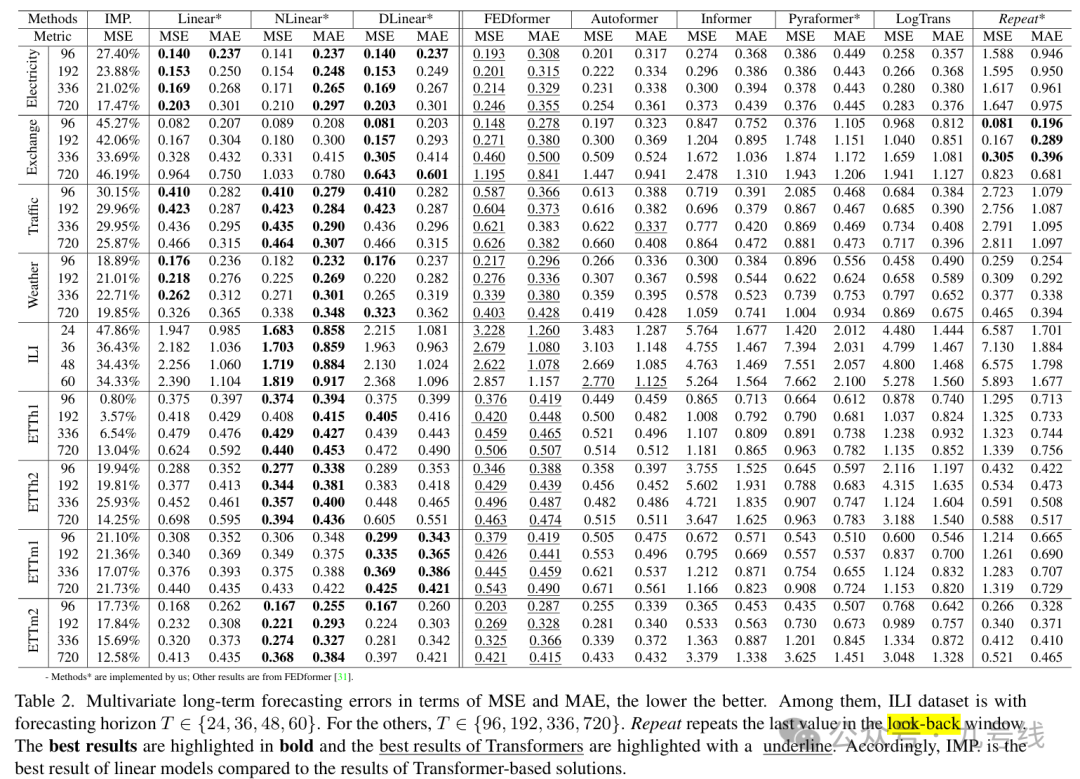
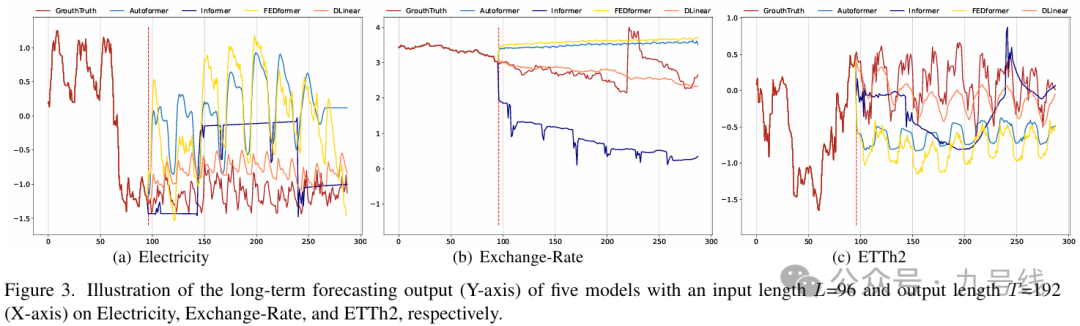
图3展示了Transformer类模型与LTSF-Linear在三个不同时间模式的数据集上的预测结果：Electricity（序列1951，36个变量）、ExchangeRate（序列 676， 3 个变量）和ETTh2（序列1241，第2个变量）。

在输入步长为96步，预测步长为336的设置下，Transformer类模型在 Electricity和 ETTh2数据上无法很好地捕捉未来数据的尺度和偏移。而在非周期性数据（如ExchangeRate）上，它们几乎无法预测出合理的趋势。这些现象进一步说明，现有基于Transformer的方案在LTSF任务中还存在明显不足。

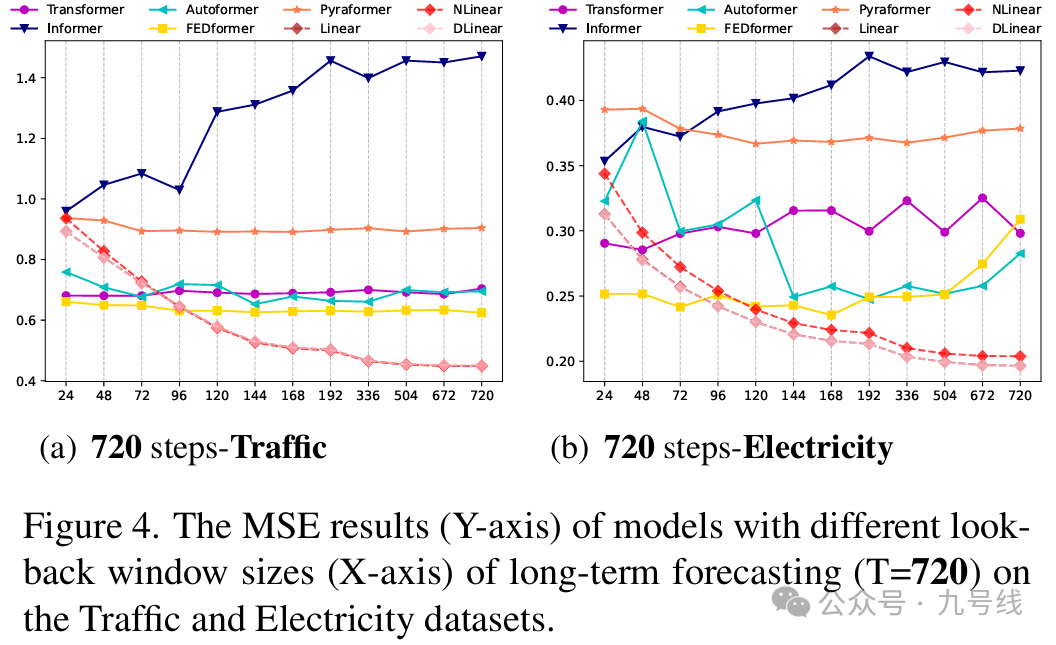
look back长度对预测精度影响很大，因为它决定了模型可以从历史数据中学习到多少信息。一般而言，一个具备强时间关系提取能力的时间序列预测模型在更长的look back下应能取得更好的预测效果。

为了研究输入look back大小的影响，作者进行了实验，设置的窗口长度为L∈ {24, 48, 72, 96, 120, 144, 168, 192, 336, 504, 672, 720}，预测步长固定为 T=720。图4展示了两个数据集上的MSE结果。从结果来看，Transformer类模型在look back增大时性能通常保持不变甚至下降。而LTSF-Linear模型在窗口增大时表现明显提升。因此，在更长的输入序列下，Transformer类模型更容易过拟合时间噪声，而不是提取时间信息。相比之下，look back设为96对大多数Transformer类模型来说是最合适的。

为了验证Transformer中复杂结构的必要性，作者以Informer（FEDformer）为例逐步做消融并简化为Linear模型：

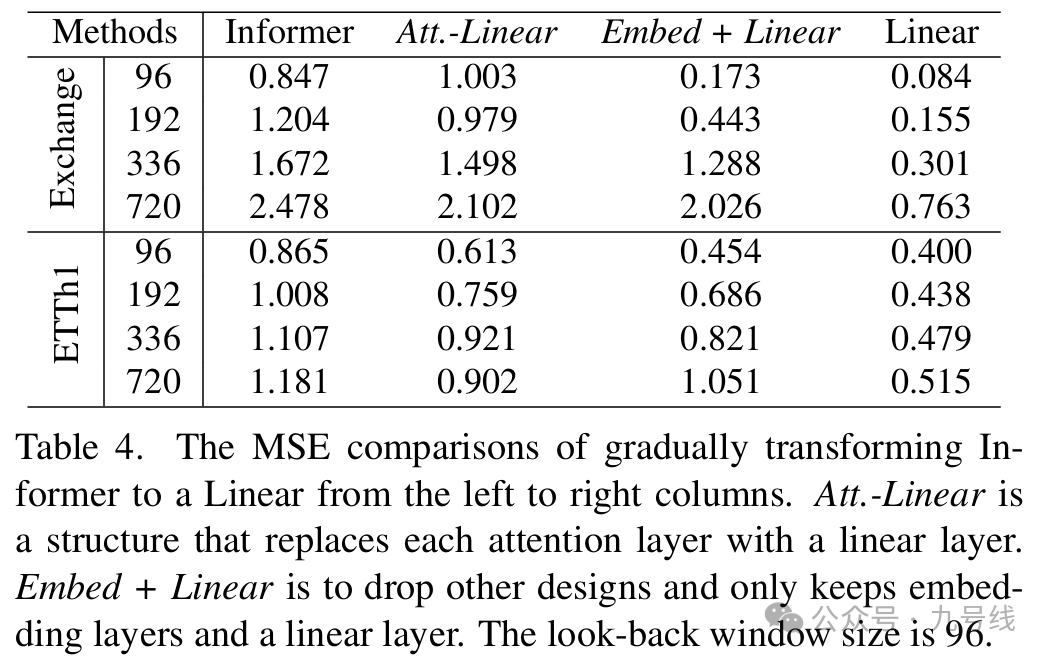
令人惊讶的是，Informer在逐步简化的过程中性能反而提升，说明在现有 LTSF基准中，自注意力机制和其他复杂模块其实并非必需（对于这点我保持怀疑，可能跟数据集选取以及其他机制有关）。

自注意力机制本质上是顺序无关的，即输入顺序不会影响输出。然而，在时间序列预测中时间顺序往往至关重要。作者认为即便引入位置和时间前面，现有的 Transformer类模型仍然存在时间信息丢失的问题。

为了验证上述想法，在进行嵌入策略之前对原始输入序列进行洗牌。文章采用两种打乱策略：Shuf——完全打乱输入序列顺序；Half-Ex——交换输入序列的前后两端。

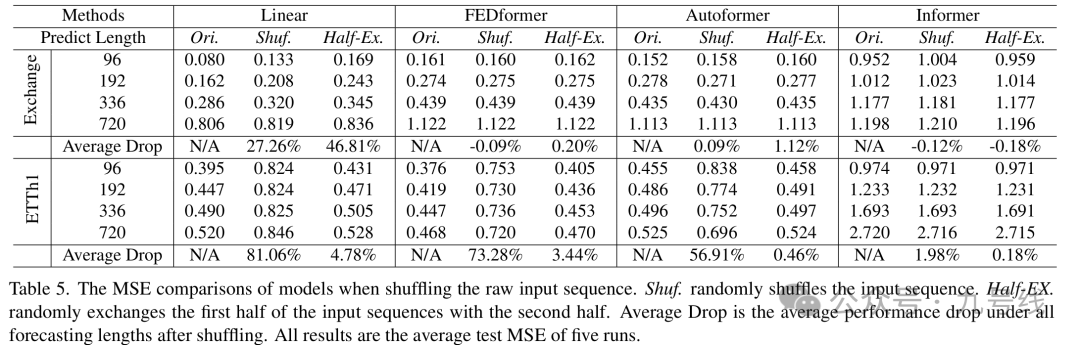
从表5可以看到，在Exchange Rate数据集中，与原始顺序相比，Transformer类模型在输入序列被随机打乱时的表现波动不大。而LTSF-Linear的性能则显著下降。这表明Transformer类模型在保留时间关系方面能力有限，更容易在噪声较大的金融数据上过拟合，而LTSF-Linear模型则能更自然地建模顺序，并通过更少的参数避免过拟合。

在 ETTh1数据集中，FEDformer和 Autoformer通过引入时间归纳偏置，在具有周期性等明确时间模式的数据上仍能提取部分时间信息。在 Shuf.设置下，它们的平均性能下降分别达 73.28% 和 56.91%。而 Informer由于缺少此类偏置，受到的影响较小。

在多数情况下，LTSF-Linear的平均性能下降幅度普遍大于Transformer类模型，表明现有Transformer类模型并不能很好地保留时间顺序（引入时间归纳偏置可解决部分问题）。

最后，针对Transformer表现差是因为训练数据规模小的观点，作者在 Traffic数据集上对比了两个不同训练集规模下模型的表现：完整数据（17544×0.7小时）和一年数据（8760小时）。如表7所示，在大多数情况下使用更少数据反而带来更低的预测误差。这可能是因为全年数据比更长但不完整的数据更具时间特性。尽管不能由此得出“使用更少数据更好”的结论，但这说明 Autoformer 和 FEDformer 的性能瓶颈并不在于数据规模。

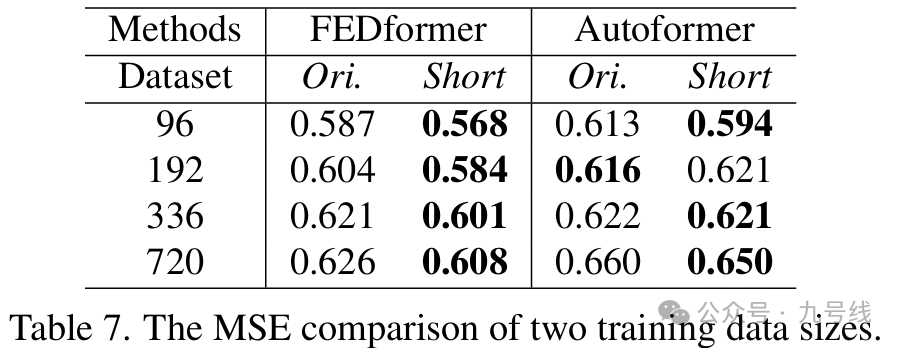
综上，作者得出结论：Transformer对时间序列的时序建模能力被夸大了：

（1）LTSF-Linear模型在多种基准数据集上表现出色，尤其在长时间预测任务中明显优于现有Transformer类模型；

（2）Transformer类模型在输入时间长度变长时，由于过拟合，性能不升甚至下降；

（3）Transformer的位置和时间戳嵌入对性能影响很大，但并不能很好地保留时间顺序信息。而LTSF-Linear模型在数据打乱（如顺序打乱）后性能大幅下降，说明它真的在“学时间信息”；

（4）Transformer的复杂结构并没有带来期望中的计算效率提升，甚至反而变慢、占用内存更多，去掉这些复杂结构后效果反而提升。

3、TimeMixer

2024年，来自阿里集团、清华大学的论文《TIMEMIXER: DECOMPOSABLE MULTISCALE MIXING FOR TIME SERIES FORECASTING》提出了基于多尺度分分解融合的TimeMixer模型，进一步提升了线性神经网络做时间序列预测的精度。

TimeMixer的整个流程如下图所示，包含三个核心模块：（1）MultiscaleTimeSeries；（2）L层PastDecomposableMixing；（3）FutureMultipredictorMixing。

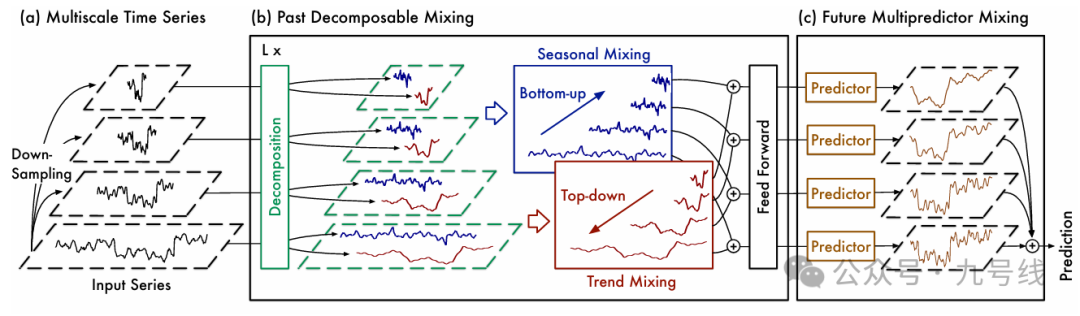
TimeMixer借鉴了TimesNet（详见《基于二维神经网络模型的一维时序预测——TimesNet系列》）的思路，将原始时间序列分解为不同尺度的子序列。但不同于TimesNet采用的FFT方法，TimeMixer直接采用下采样方式，将原始输入序列X∈R_p*c转换为不同周期尺度的子序列X_m∈R_[p/2^m]*c。此处p是序列长度、c是变量个数，m表示第m个尺度。比如m=0的时候，X_0就是原始序列。

然后将分解后的不同周期尺度序列进行Embedding，包括纳入时间戳的Embedding，这个操作在上面的流程图中没有体现。X={x_0,··· ,x_M}输入PastDecomposableMixing模块，该模块首先将各个子序列拆解为季节项（seasonal）和趋势项（trend），然后对不同尺度的季节项和趋势项融合汇总。

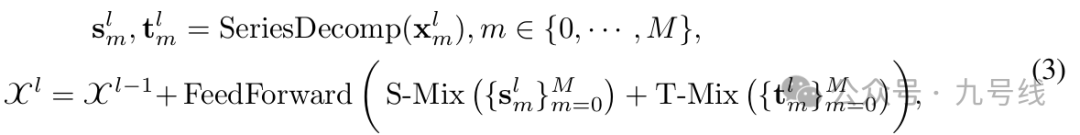
不同尺度的季节项和趋势项怎么融合呢，对于季节项，作者用两种相反的方式来分别处理不同尺度的趋势项和不同尺度的周期项的融合，如下图：

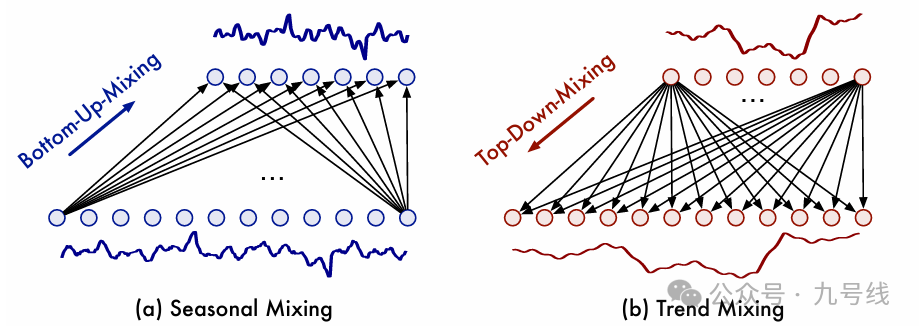
对于季节项，作者采用自下而上的方法（BottomUp）融合，即从较低层次的细尺度时间序列向上吸收信息，可以为较粗尺度的季节性建模补充详细信息。因为细颗粒度周期本身就包含了粗颗粒度周期，比如7天构成1周、4周构成1月、3个月构成1季度。

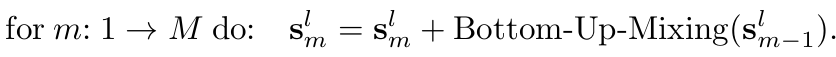
对于趋势项，采用类似的方法融合。由于上层的粗颗粒度时间序列比下层的细颗粒度时间序列更容易提供清晰的宏观信息。因此，趋势项采用自上而下（TopDown）的融合方式，以利用粗尺度的宏观知识来指导细尺度的趋势建模。

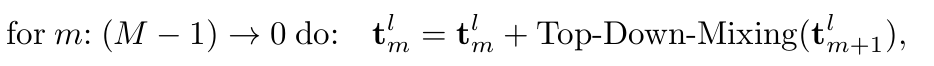
PastDecomposableMixing模块的最后一步FeedForward包括两个线性层，主要用于提取不同变量间的交互信息。所以TimeMixer既考虑了同一变量不同尺度间的交互、也考虑了不同变量间的交互（模型提供了一个参数，可以设置为变量间交互或不交互）。

将经过L层PastDecomposableMixing模块迭代后的X_L输入最后的FutureMultipredictorMixing模块进行预测，得到预测值：

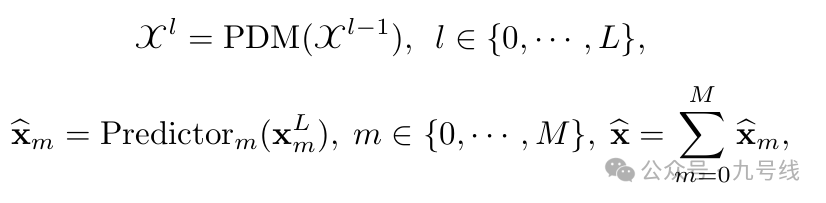
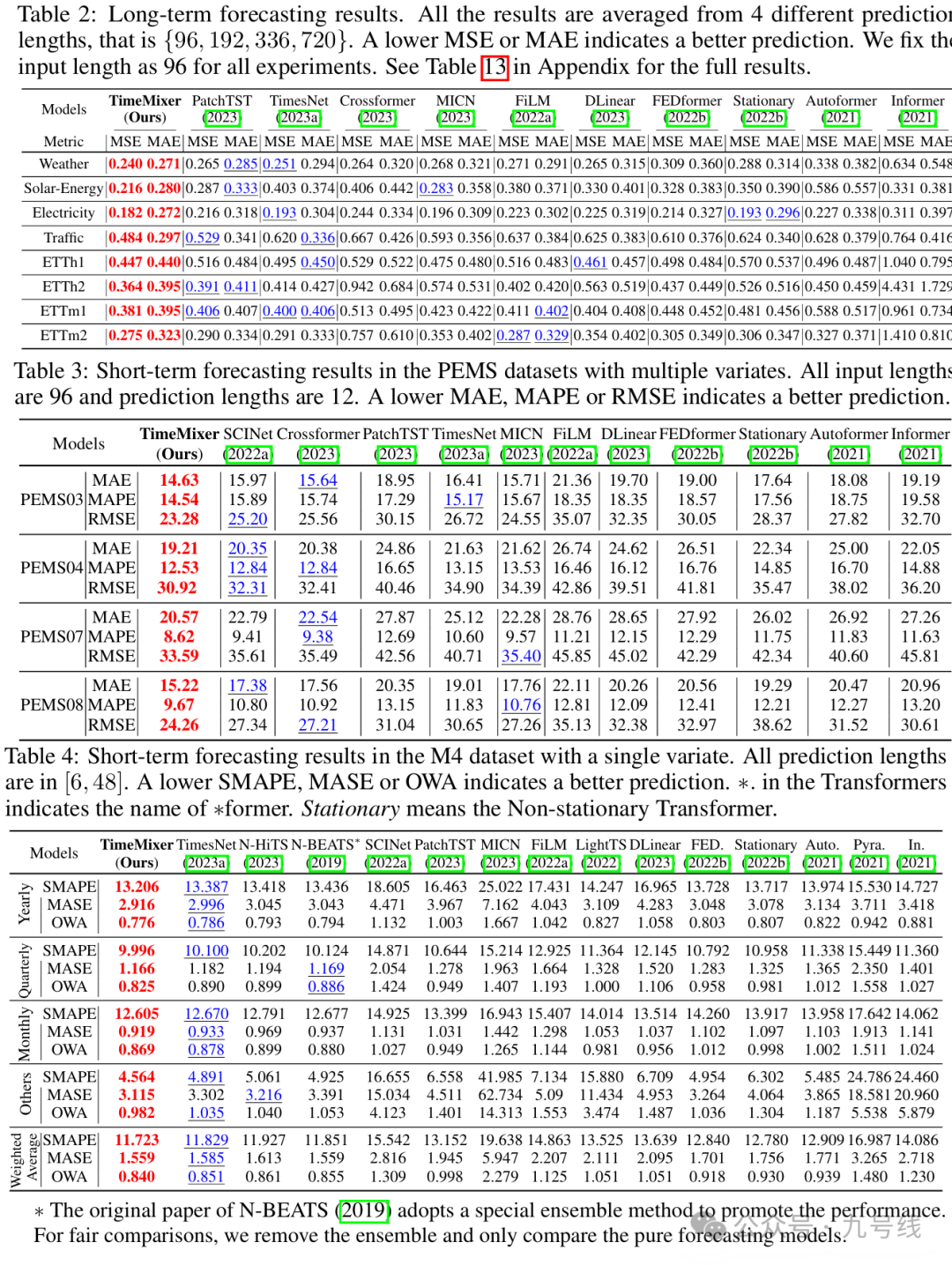
在长期序列预测、短期多变量预测、短期单变量预测等多个任务上，TimeMixer均表现出了更好的预测效果。

二、基于Transformer的时序预测模型

Transformer类时序模型应该是被魔改得最多的一类，这里介绍几个比较新且效果还不错的模型。

1、PatchTST

2023年ICLR上，普林斯顿大学和IBM研究所共同发布的论文《A TIME SERIES IS WORTH 64 WORDS—LONG-TERM FORECASTING WITH TRANSFORMERS》提出了PatchTST模型。

看到题目第一反应是联想到Vision Transformer的论文《An Image is Worth 16x16 Words: Transformers for Image Recognition at Scale》，两者思路有点像，都是将时间序列或者图片切成块（patch）后输入Transformer模型。

PatchTST的工作流程很简单，把一个M维输入系列x∈R_M*L拆分得到M个1*L长度的序列，分别输入Transformer模块，预测后再合并成一个M*T的变量，其中L是输入步长、T是预测步长。

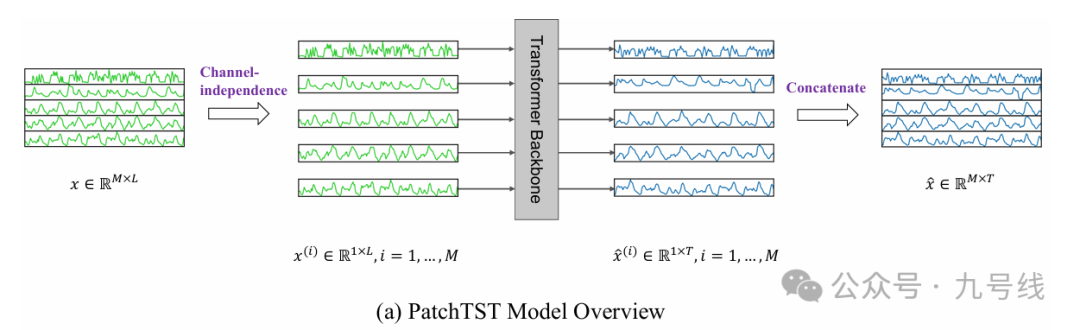
整个网络的核心部件是中间的Transformer Backbone模块，作者提出了两种构架，一种是监督学习、另一种是自监督学习。

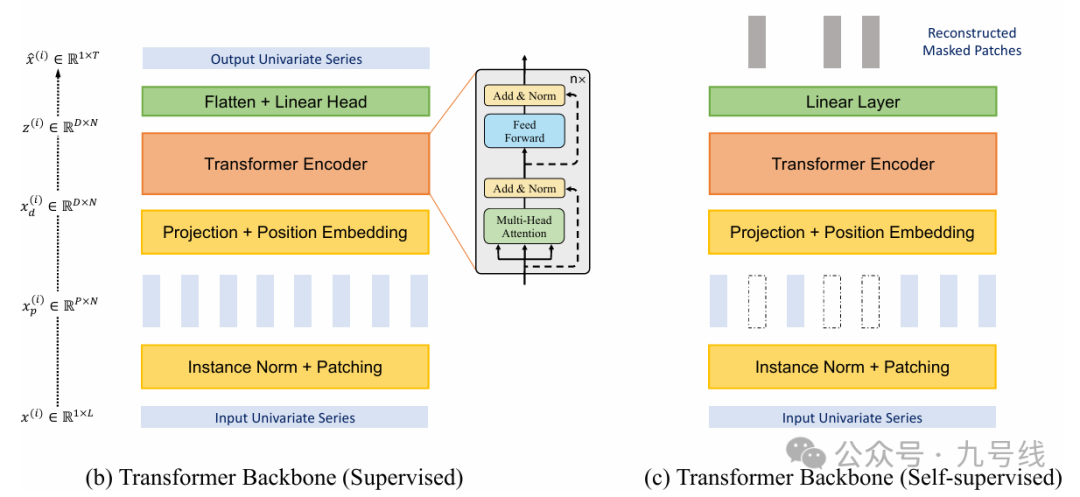
监督学习（Supervised）构架的工作流程：

（1）首先将输入序列x_i∈R_1*L标准化，然后以长度P，步长S（每个patch可能重叠也可能不重叠，取决于P和S的取值）对序列进行Patching操作，得到的patch数量N = [(L−P) /s] + 2。通过patch，输入的数量可以从L减少到大约 L/S，大大降低了后面多头注意力机制的计算复杂度；

（2）对每个patch进行向量编码和位置嵌入；

（3）将嵌入后的patch输入TransformerEncoder；

（4）将TransformerEncoder的输出展平并做一个线性映射，得到预测序列x_hat_i∈R_1*T；

自监督学习（Self-Supervised）构架的工作流程：

（1）同样首先将输入序列x_i∈R_1*L标准化，然后以长度P，步长S（每个patch可能重叠也可能不重叠，取决于P和S的取值）对序列进行Patching操作，得到的patch数量N = [(L−P) /s] + 2。通过patch，输入的数量可以从L减少到大约 L/S，大大降低了后面多头注意力机制的计算复杂度；

（2）随机抽取部分（Maked）patch将其对应向量设置为0；

（3）对每个patch进行向量嵌入和位置嵌入；

（4）将嵌入后的patch输入TransformerEncoder学习特征表示；

（5）学习到的特征表示通过线性层映射回patch向量，并和真实的（Masked）patch向量对比；

（6）持续上述过程，更新模型参数。

自监督学习网络主要学习的是特征表示！！！

下图展示了监督学习构架下，PatchTST和其他主流模型的预测效果。其中PatchTST/64表示输入为512，patch长度64，滚动步长S为8；PatchTST/42表示输入为336，patch长度16，滚动步长S为8。

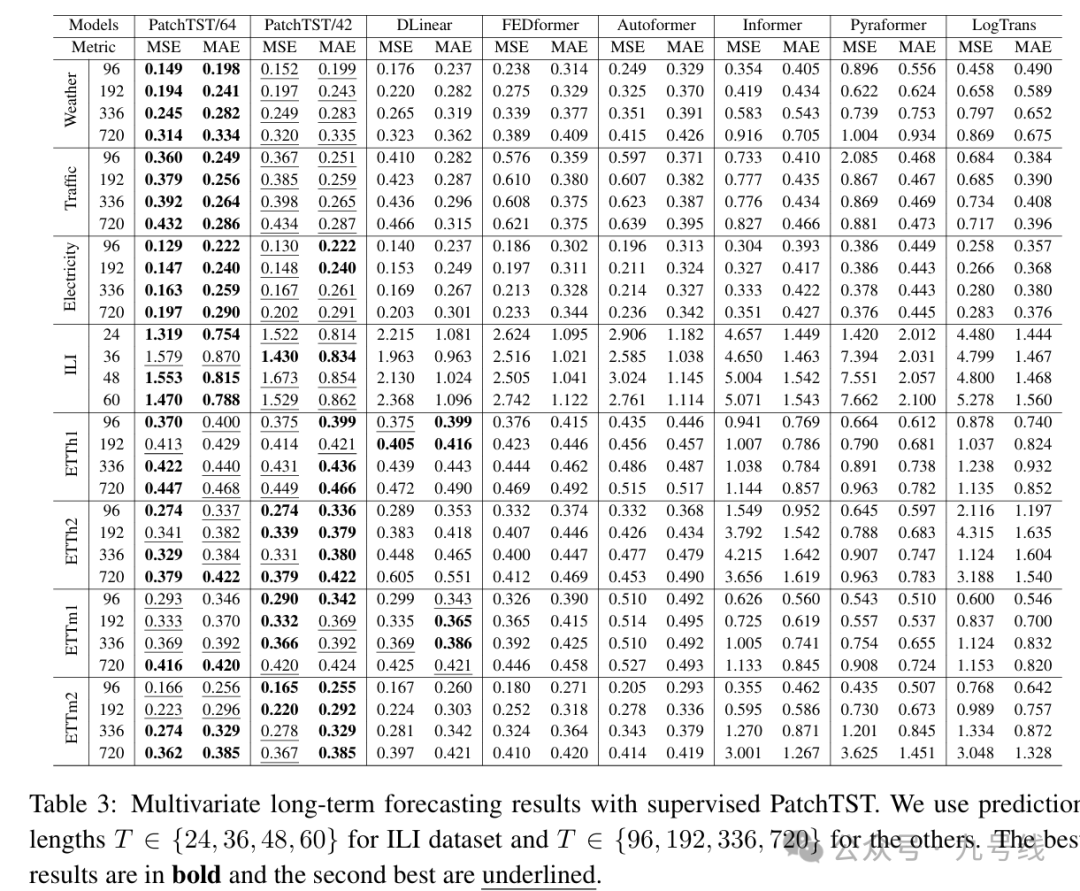
如果采用自监督流程，进行下游预测任务时通常有两种方法：（a）使用自监督训练得到的网络模型进行下游任务预测，预训练得到的表征学习网络参数固定，即linear probing；（b）使用自监督训练得到的网络模型进行下游任务预测，过程中预训练得到的表征学习网络参数也会更新，即end-to-end fine-tuning。理论分析表面后面的方法效果更好。

作者将自监督流程和监督流程（PatchTST/42）两种模型进行了对比，采用自监督流程的模型预测效果略好于PatchTST/42。

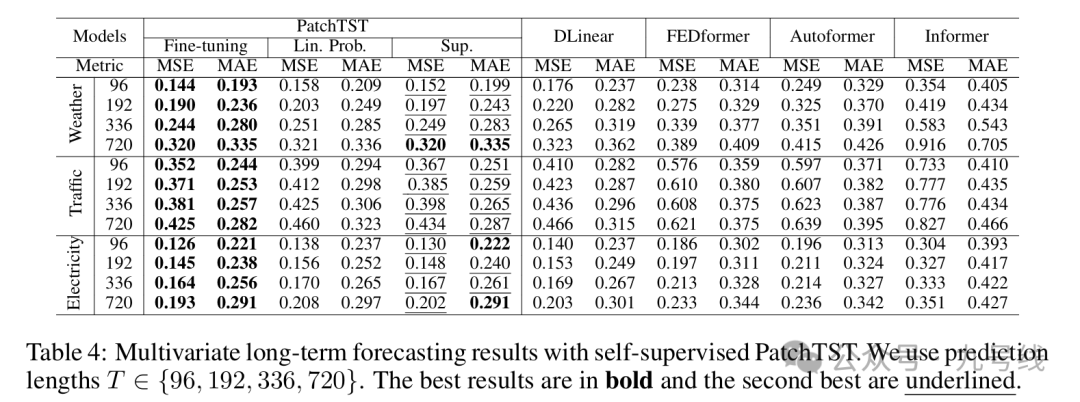
PatchTST作为Transformer的改进版，提出了将时间序列切分成patch作为Token输入的思路，提高了模型的训练效率和预测精度。但它的问题也显而易见：

（1）固定patch。PatchTST/64或PatchTST/42将长度L的序列根据固定patch长度64、滚动步长S=8切分为N个Patch，难以捕捉到序列中存在的其他周期特征，作者也没有尝试更多的patch取值；

（2）通道独立。PatchTST为每个变量单独建模预测，无法捕捉到跨变量的相关信息。

2、CrossFormer

为了解决上述PatchTST中的两个问题，上海交大人工智能实验室发表了CROSSFORMER:TRANSFORMER UTILIZING CROSS DIMENSION DEPENDENCY FOR MULTIVARIATE TIME SERIES FORECASTING》一文，提出了CrossFormer模型。

这里的Cross即为时间维度和变量维度的双重信息融合，具体通过三个过程实现：DIMENSION-SEGMENT-WISE EMBEDDING、TWO-STAGE ATTENTION LAYER、HIERARCHICALENCODER-DECODER。

（1）DIMENSION-SEGMENT-WISE EMBEDDING

主要是对原始输入序列按时间维度进行切割以及加入向量和位置嵌入，其中L_seg是切割的步长，D是时间序列的变量维度。

（2）TWO-STAGE ATTENTION LAYER

对于DSW的输出H或者上一层的输出Z（CrossFormer采用多层编码、解码结构，后面会解释），直接应用自注意力会产生二次方的复杂度，因此作者通过两阶段注意力层捕获二维数组跨时间和跨维度的依赖性。

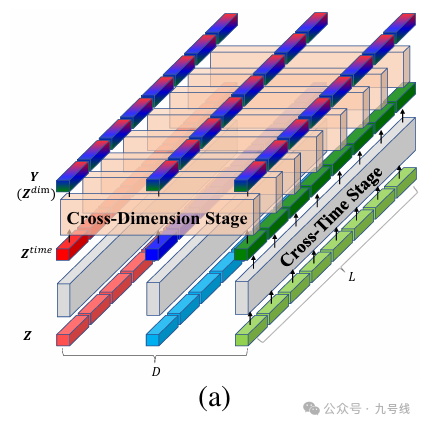
首先进行跨时间片段的信息融合，作者直接对每个维度应用了多头自注意力，这里Z_i,: 来表示时间片段i对应的所有维度的向量，用Z_:,d表示维度d上所有的时间片段。

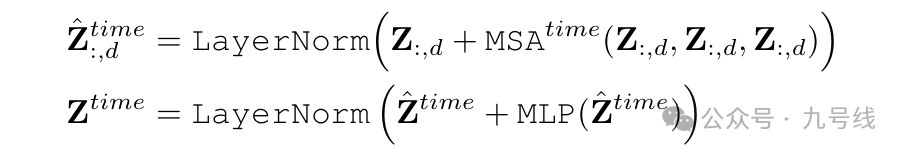
得到的Z_time融合了每个维度的跨时间信息，接着对其进行跨维度信息融合。在跨维度阶段，直接使用注意力机制将导致计算复杂度达到O(D^2)，尤其当D相当大的时候。

为了应对这个问题，作者提出了一种路由器（降维）机制：首先为每个时间片段i设置一个固定的（远小于D）的可学习向量作为路由器，即R_i：。将路由器R_i：作为查询Q，将Z_time_i：作为K和V进行第一次多头自注意力计算。然后，路由器将收集到的信息B_i：按照维度分发，这一过程中将Z_time_i：作为Q，而聚合后的信息B_i：作为K和V进行第二次多头自注意力计算。通过此方法，作者构建了D个维度间的全面连接关系。

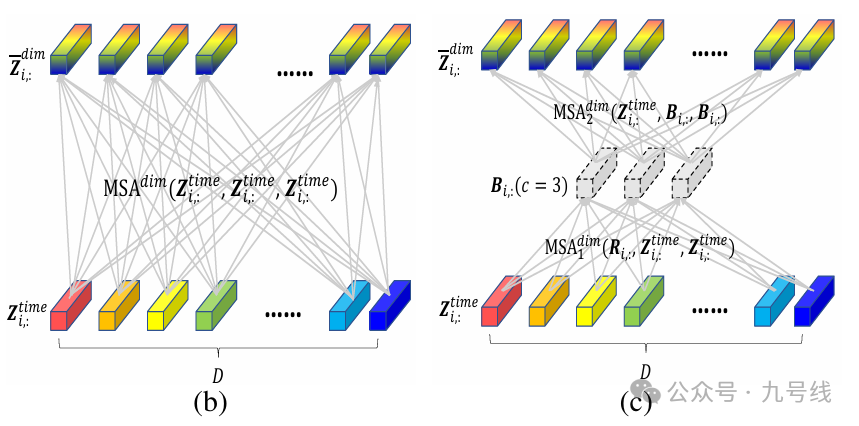
最后的输出Z_dim∈L*D*dimmodel。

（3）HIERARCHICALENCODER-DECODER

在CrossFormer中，上述提到的TSA模块内嵌于一个多层的编码解码器结构中。

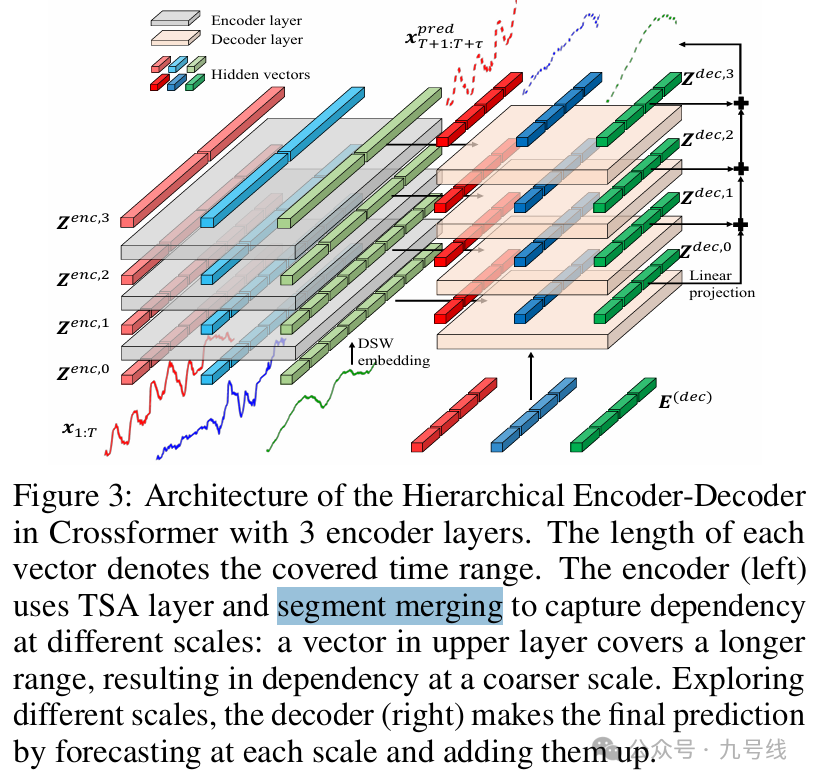
在encoder的每一层，除了第一层外（第一层就是DSW的输出H），其余层每相邻的两个时间片向量被合并以捕捉不同时间尺度上的信息交互，最后通过TSA层捕获依赖性，得到该层的encoder输出z_enc,l。

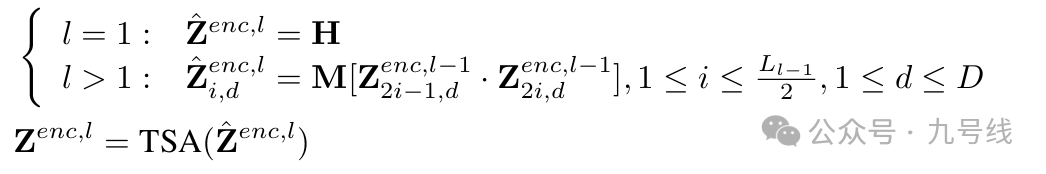
在decoder的每一层，除第一层外，其余每层首先对上一层decoder的输出z_dec,l-1进行TSA计算，并以同一层encoder的输出z_enc,l作为key和value进行一次多头自注意力计算，并进行相应的标准化和线性操作后得到该层的decoder输出z_dec,l。需要注意的是decoder的第0层中的E（dec）∈（τ/RLseg）*D*dimmodel是一个可学习的嵌入向量，此处τ对应的是预测时间序列的长度。所以解码器的输出z_dec,l同样是一个（τ/RLseg）*D*dimmodel的结构。

最后对每一个z_dec,l进行线性映射并取平均值，即可得到最终的预测序列x_pred。

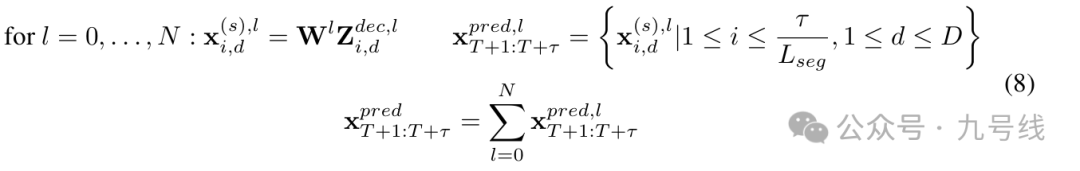
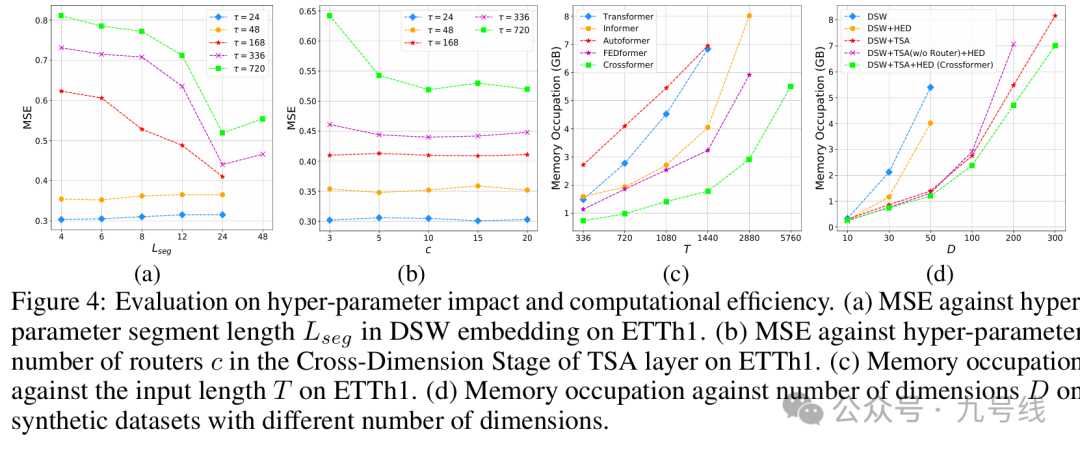
CrossFormer兼顾了时间序列上不同尺度间的信息以及不同变量间的相关信息，因此相较于过去的Transformer类模型，取得了更好的预测效果。

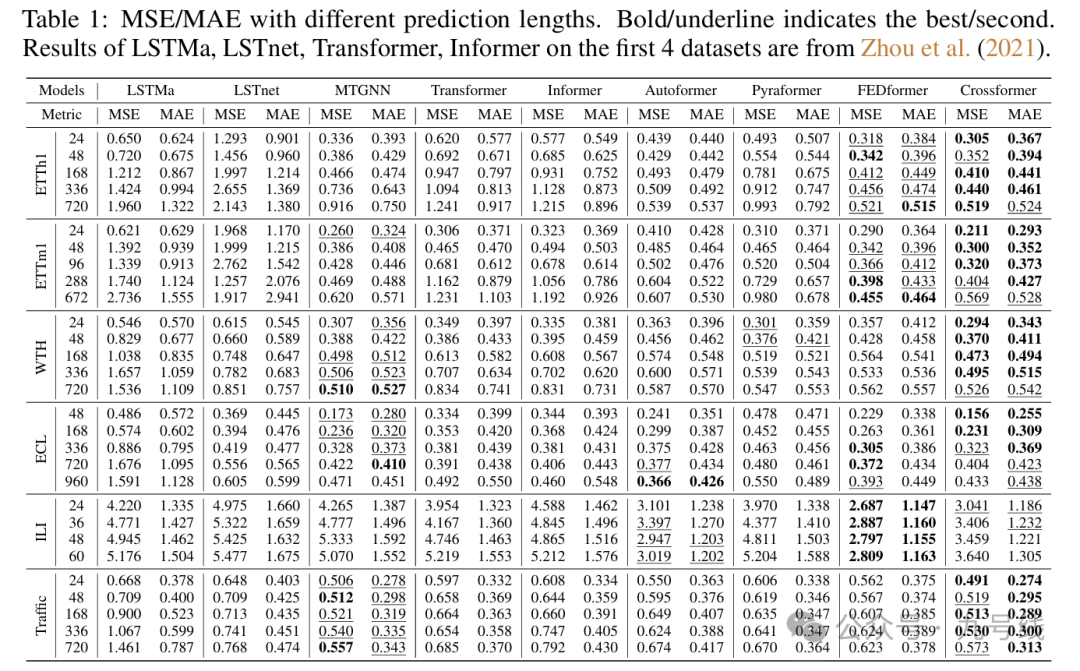
CrossFormer模型的主要参数是时间分割长度L_leg和路由器数量c：对于短期预测（24、48）来说预测精度总体较稳定，对于长序列预测（168及以上），分段长度越长预测效果越好。此外在超长序列（720）预测中c的增加会导致MSE的下降。

3、iTransformer

2024年，来自清华大学的论文《INVERTED TRANSFORMERS ARE EFFECTIVE FOR TIME SERIES FORECASTING》提出了一个全新的Transformer魔改模型——Inverted Transformer。

根据是否修改组件以及是否修改结构，作者将目前的Transformer类时序预测模型划分为四大类，前面介绍的PatchTST和CrossFormer分别属于第二第三象限类别，而iTransformer属于第四象限类别，即只修改结构但不修改任何组件。

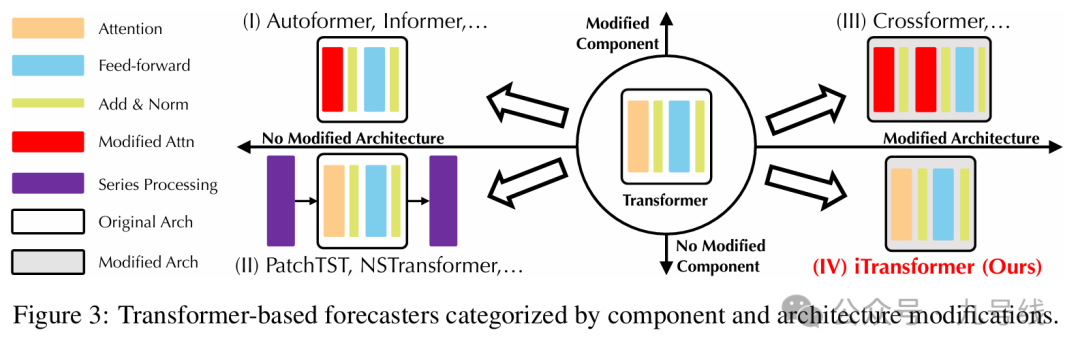
作者认为传统Transformer类模型没有充分考虑变量间差异及相关性，以往方法将所有变量在同一时刻的时间点表示为一个词（Temporal Token），但由于其过小的感受野和变量间内生滞后期，这类词较难揭示足够丰富的语义甚至包含噪声干扰，限制了注意力机制建模词之间关系。另外，来自不同变量的时间点被映射到词表示后，原本独立的变量被杂糅为多维特征，使模型无法显式区分并捕捉变量间关联。

不同于之前的Transformer类模型，iTransformer将单一变量的一整条历史序列作为一个token输入Transformer模型。某种程度上，iTransformer可以理解为PatchTST的特殊版本（patch长度=整条序列长度），所以看到一些评论说论文的结果与PatchTST相比要弱一些。

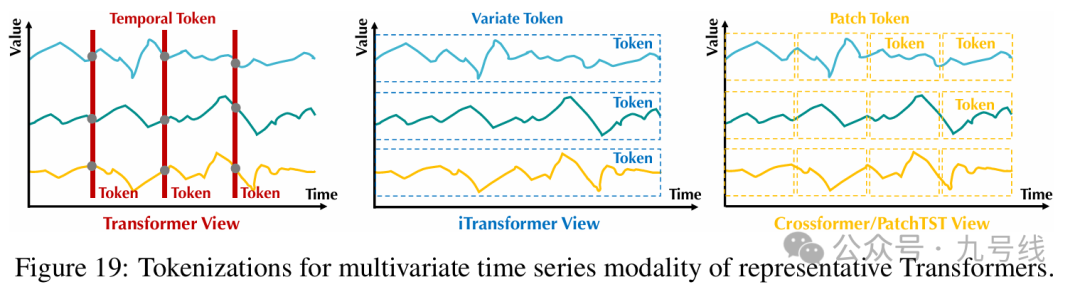
iTransformer基于编码器（Encoder-only）结构，工作流程如下图。整个网络包含了三个组件：嵌入层（Embedding）、L层的Transformer模块（TrmBlock）以及最后的预测映射层（Projection）：

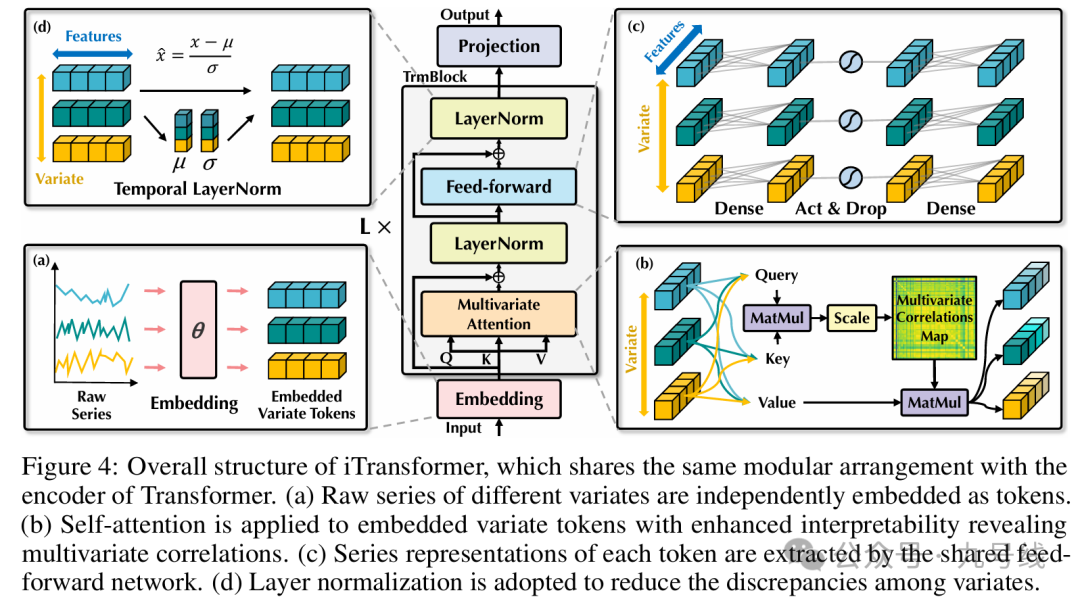
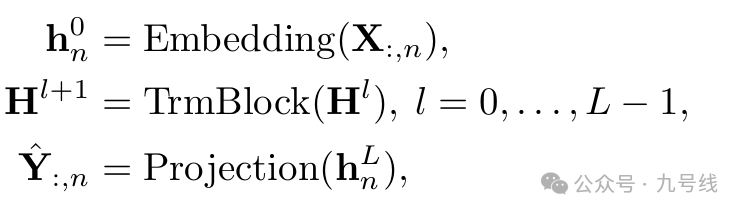
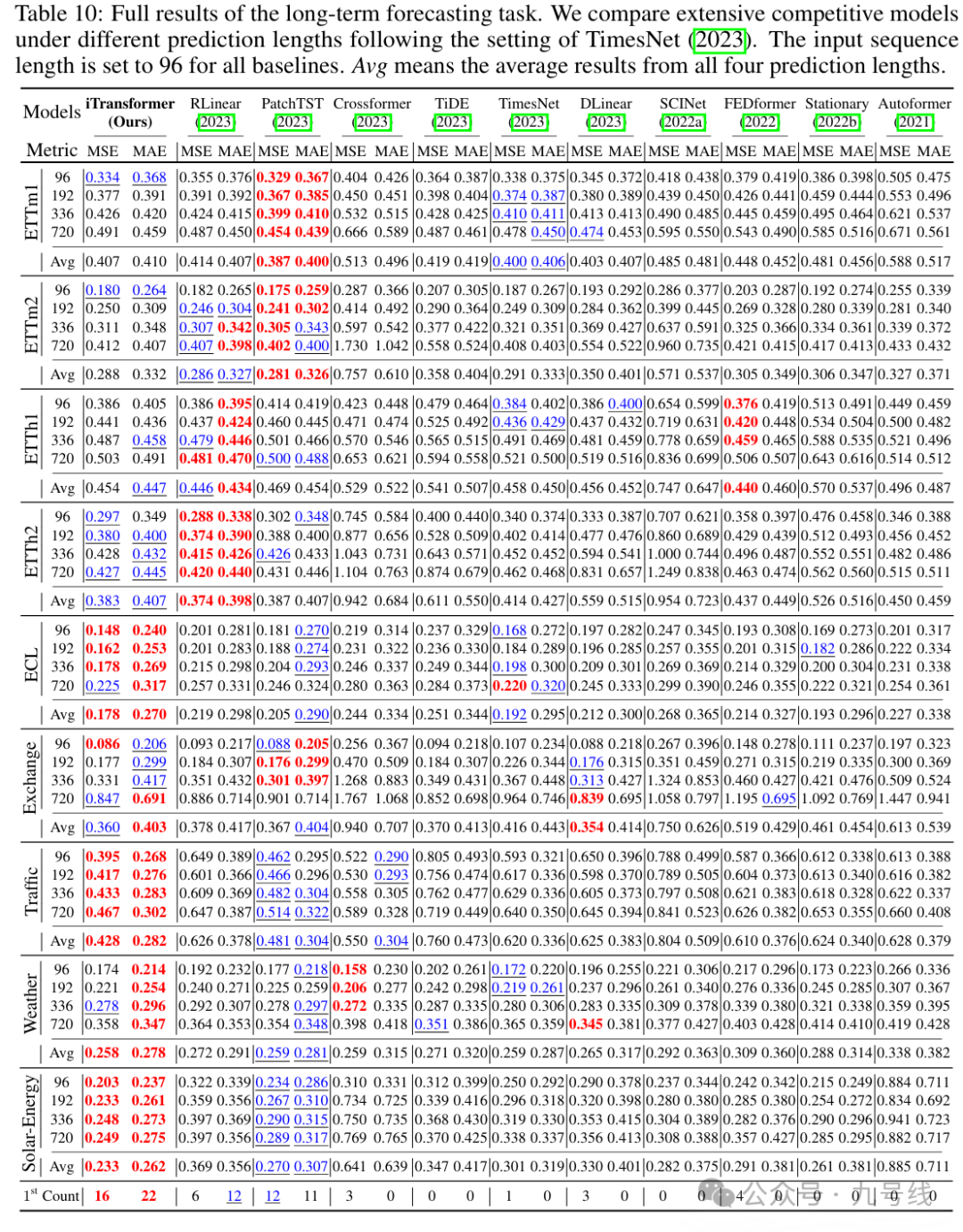
从实验结果来看，仅仅以变量维度作为token输入Transformer模型就能取得比之前模型更优的预测效果，在部分数据上（如Traffic、Weather、Solar-Energy等）的预测效果甚至超越了PatchTST，有点不可思议。

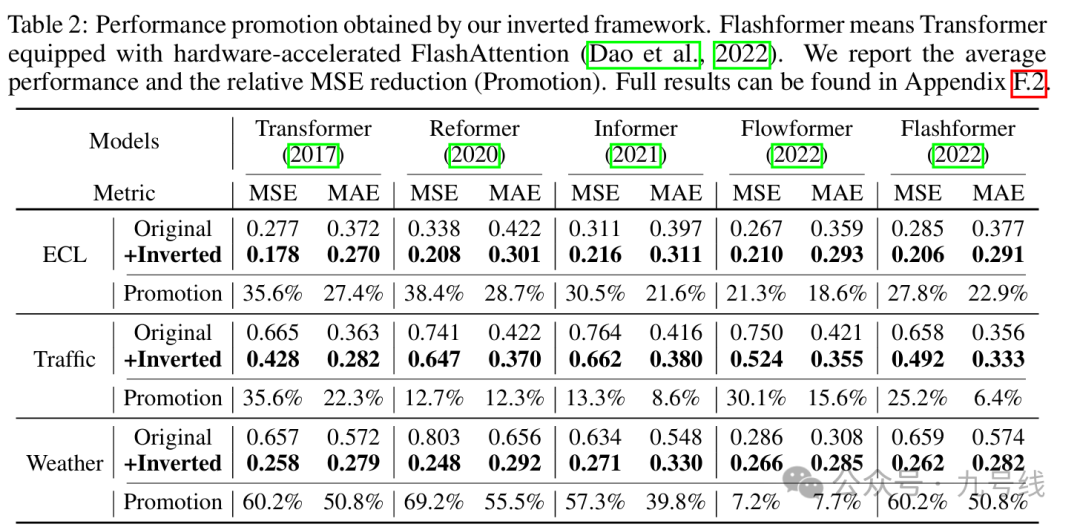
对传统Transformer类模型按变量维度建立token，修改后模型的预测效果较倒置前均取得了大幅度的提升，也证明了以变量维度建立token能更好捕捉到变量之间的信息。

以Traffic数据集为例，每个变量（sensor）表示某个街区的道路堵塞情况，通过可视化发现变量间存在着显著的同步关系（如Sensor 2和2）以及领先滞后关系（如Sensor859和861），一定程度解释了传统Transformer类模型失效的原因（仅仅聚合同一时刻但在事件描述上并未对齐的变量作为token）。

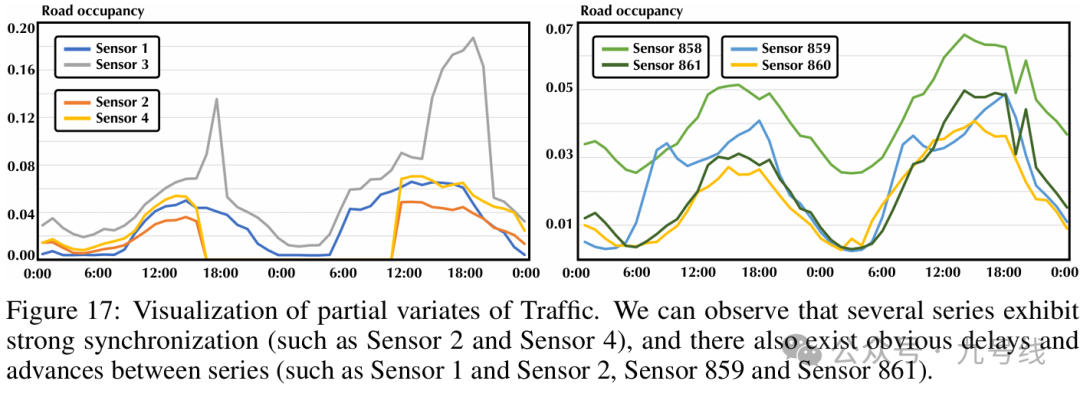
另一个有趣的实验是，iTransformer模型在推理时可以输入不同于训练时的变量数，即仅使用部分变量训练的模型就能够取得较低的误差，证明倒置结构在变量特征学习上的泛化性。

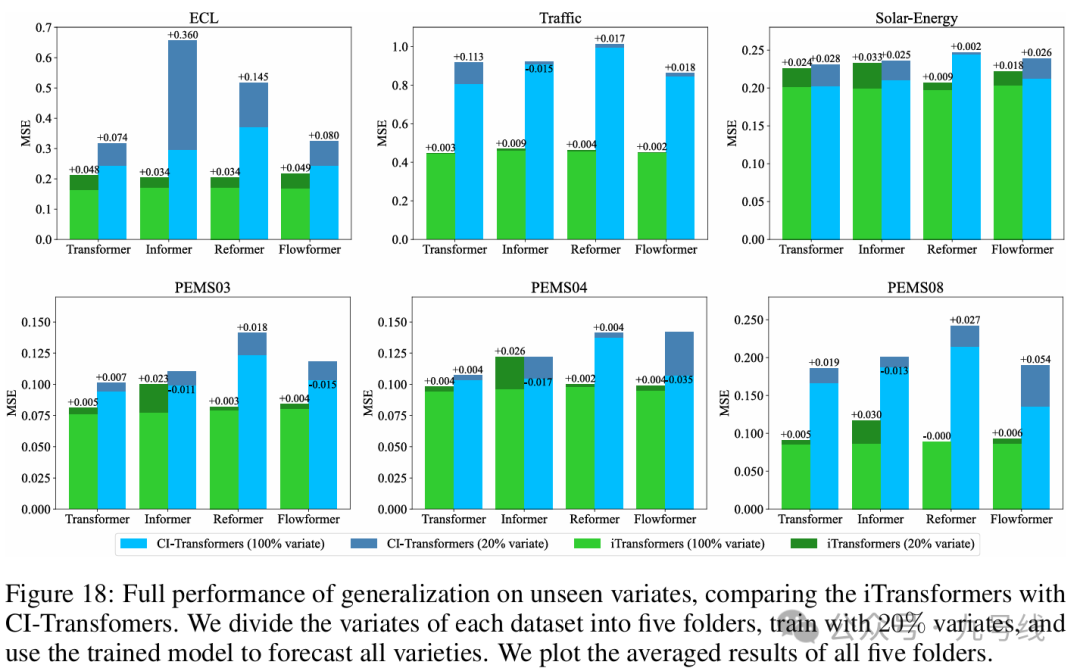
前面介绍DLinear/NLinear时曾提到过，传统Transformer模型另一个被人诟病的问题就是预测效果不一定随着输入的历史步长的变长而提升。在使用倒置框架后，模型随着历史观测长度的增加，预测误差呈现明显降低趋势。

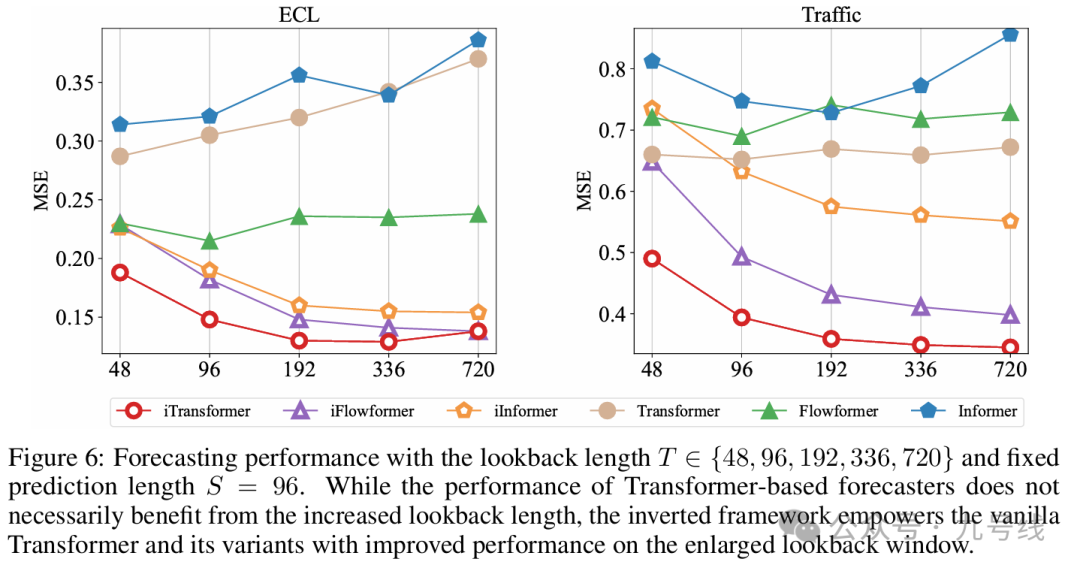
三、基于CNN的时序预测模型

将CNN运用到时序预测的主要思路是运用1D或2D卷积网络提取时间序列分解后不同尺度下的周期。

1、TimesNet

关于TimesNet的详细介绍可参考之前文章《基于二维神经网络模型的一维时序预测——TimesNet系列》，这里简单过一下。

《TIMESNET: TEMPORAL 2D-VARIATION MODELING FOR GENERAL TIME SERIES ANALYSIS》发表于2023年的ICLR，其背后动机来自于现实生活中的许多时间序列表现出多种跨周期性变化。比如温度的周期性变化，以日为单位通常白天比晚上热，以季为单位通常夏季比冬季热，这里就牵涉到周期内不同时段的温度变化，以及周期间同一时段的温度变化（夏季早晨比冬季早晨热）。所以TimesNet提出在二维空间中重塑时间序列，以模拟周期内和周期间的变化。

整个模型的流程如下图所示，核心组件是timesblock，包括三个重要部分：

1、FFT；2、Inception blcok；3、Adaptive Aggregation

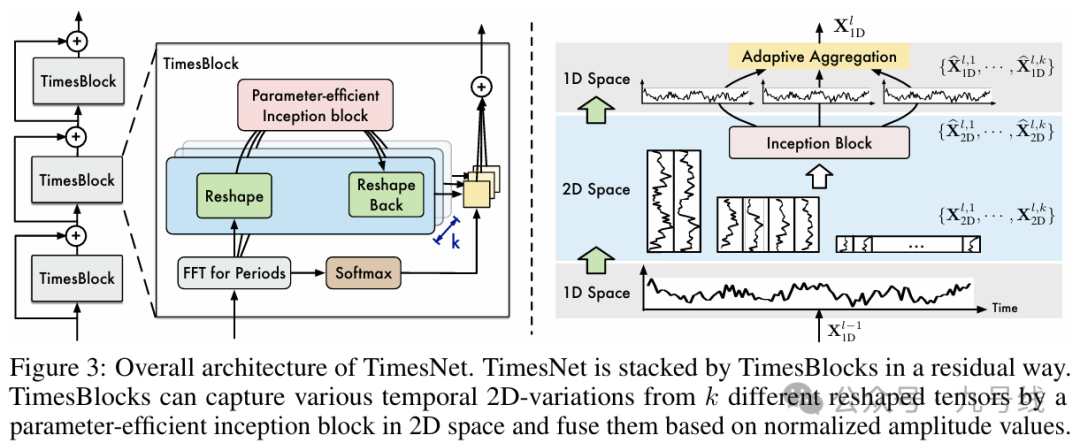
1、首先原始时间序列（多变量N*L或单变量1*L）通过FFT（快速傅里叶变换），提取原始时间序列中的不同划分形式，如下图所示。以一年365天举例，如果以周为周期一年就有52个周期、如果以月为周期一年就有12个周期、如果以半年为周期一年就有2个周期，以此类推可以有各种划分方法。

对一个长度为T的时间序列，理论上可以提取出T/2中周期划分方式。不过为了提取最有价值的信息，通常会提取幅度（Amplitude）最大的K个周期。

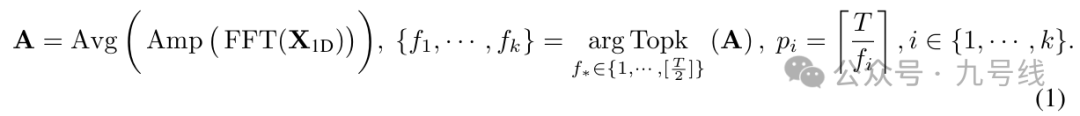
然后通过reshape方式为每个周期创建对应的2D向量，比如对于周数据就是5（day）*52（week），月数据就是30（day）*12（month）等等，如下图所示。

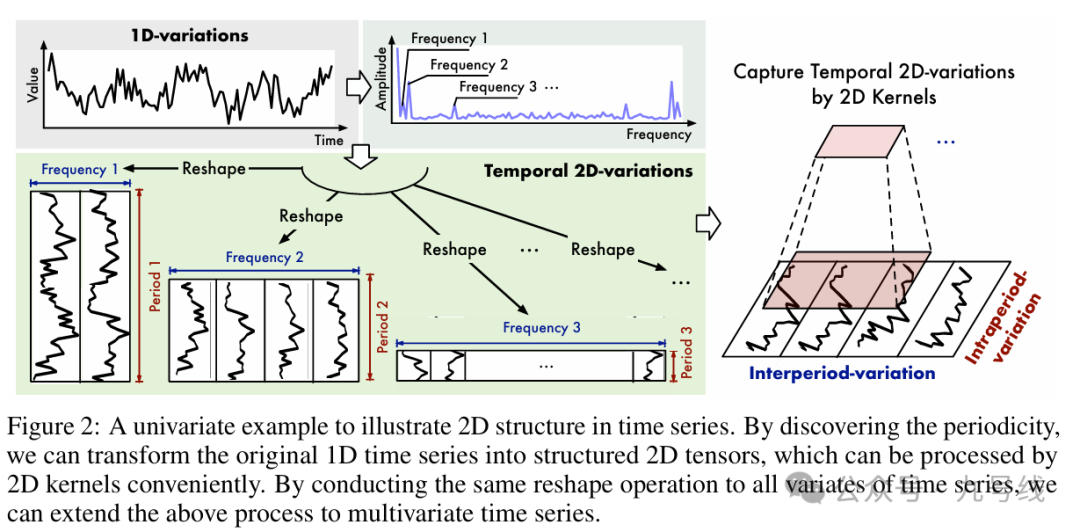
2、将这些2D向量输入2D卷积神经网络提取图片特征以捕获时间变化。在TimesNet中，数据被发送到Inception-V1模块（又称GoogleNet，最新版本是V4），结构如下图。关于Inception模块的具体结构和工作原理在文章《常见图像分类神经网络模型梳理》中有详细介绍。

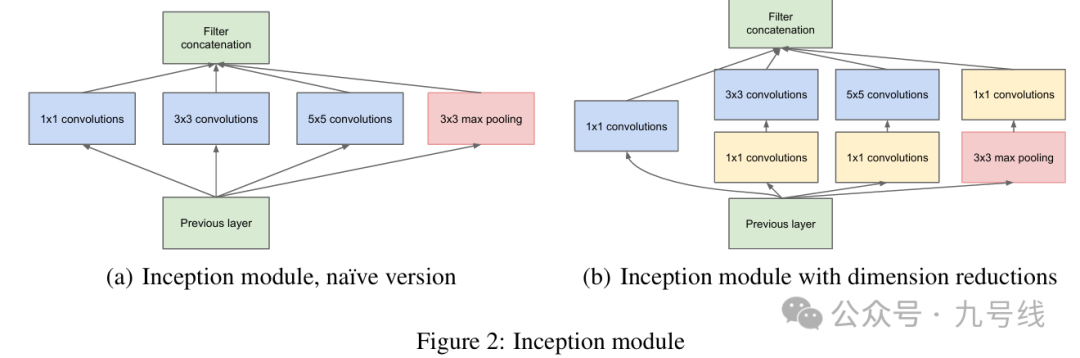
3、通过reshape将Inception模块输出的2D向量重新转换为1D向量，然后通过Adaptive Aggregation将这些1D向量加权相加，权重为每个周期对应的振幅。整个模型的工作流程可以用如下公式表达：

无论是长期预测还是短期预测，TimesNet的表现都要优于传统基于RNN的模型（LSTM表现太差甚至都没有展示）和基于Transformer的模型。在金融时间序列Exchange上，TimesNet的预测效果不如DLinear。

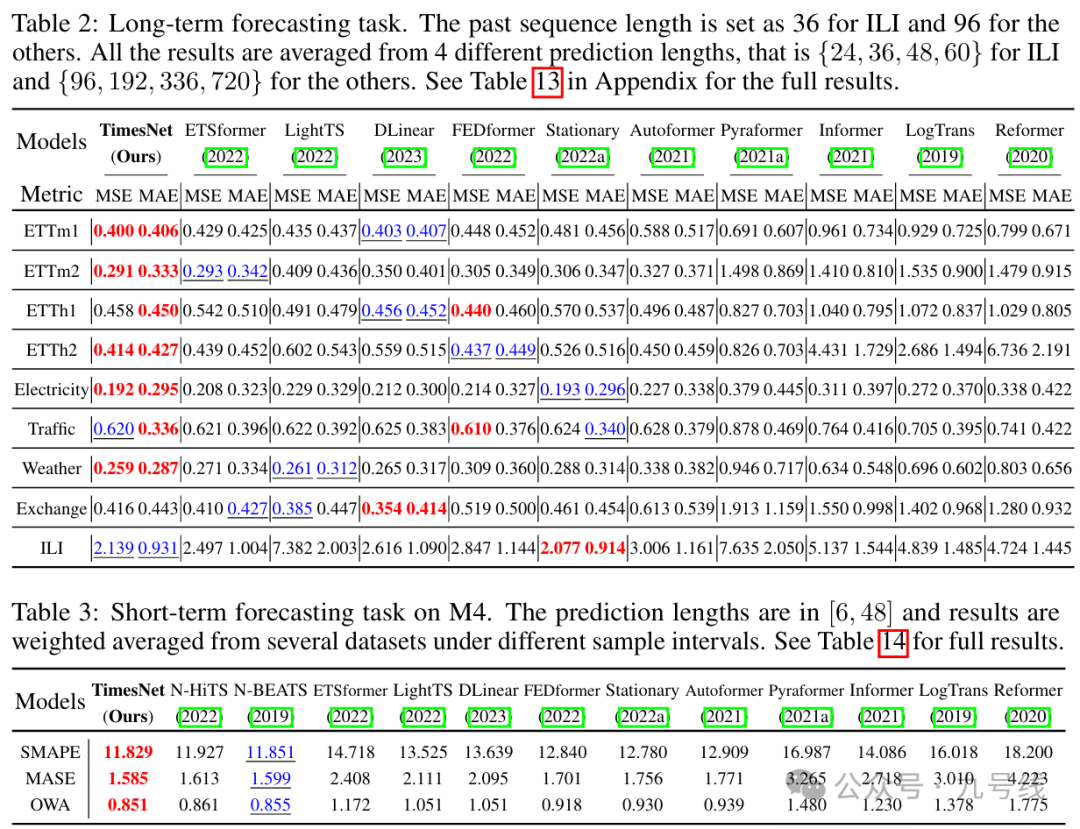
2、MICN

MICN同样来自一篇2023年的ICLR论文，由四川大学发表的《MICN: MULTI-SCALE LOCAL AND GLOBAL CONTEXT MODELING FOR LONG-TERM SERIES FORECASTING》。模型的创新点主要在于将序列拆分为季节性和趋势性，然后对季节性序列进行多模态建模并预测。整个模型的流程图如下：

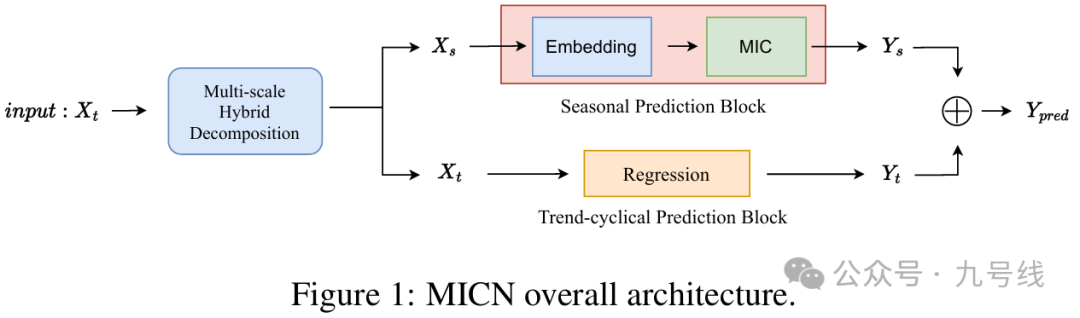
原始输入序列首先通过MULTI-SCALE HYBRID DECOMPOSITION模块进行分解得到Trend-Cyclical项和Seasonal项。这里作者采用平均池化先得到Trend-Cyclical项，然后从原始序列减去Trend-Cyclical项得到Seasonal项。考虑到平均池化的参数kernel大小控制着分解的不同模式，因此取多个kernel的平均池化结果，得到Trend-Cyclical项和Seasonal项：

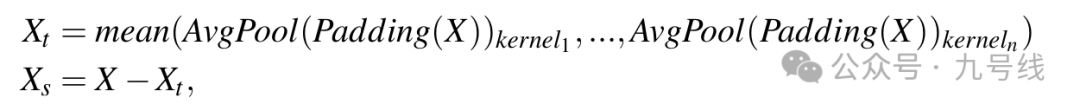
对于趋势项X_t预测模块，作者直接采用线性回归或者均值方式计算对应未来的预测值Y_t

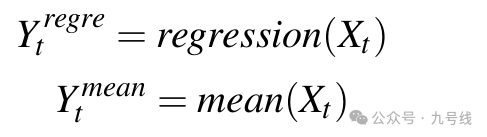
对于季节项X_s预测模块，包括一个Embedding模块和N层MIC，内部流程图如下。

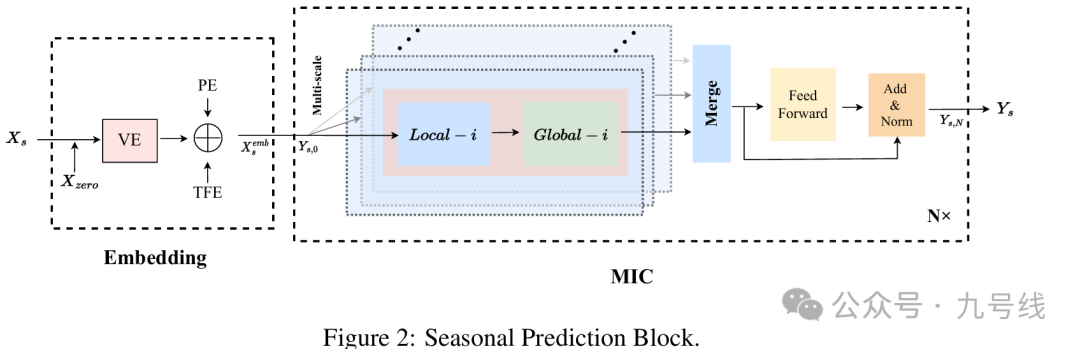
首先对输入X_s进行Embedding：

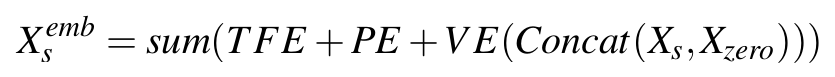
每一层MIC内部，都含有i个代表不同尺度的Local—Global模块，如上图中浅蓝色部分所示。对于每一层MIC，首先将不同尺度的序列输入多个Local-Global模块计算。Local—Global模块是MIC的核心组件，内部分别由一个由聚合局部特征的Local模块和聚合所有局部特征之间关系的Global模块串联而成。

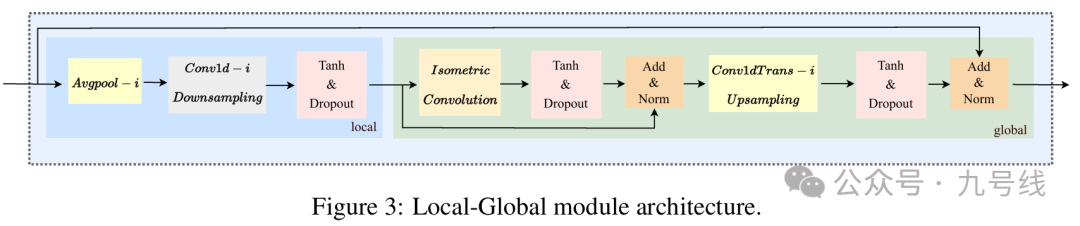
对于Local模块，首先使用kernel大小为i的平均池化层平滑噪声，然后使用kernel大小为i、stride大小也为i的1D卷积来进行降采样，相当于将序列长度缩小了i倍，i的取值范围为（I/2，I/4，I/8。。。。这里I是输入序列的长度）。

对于Global模块，它的输入是上一步骤得到的降采样后序列，该序列已经融合了序列的局部特征。接着采用Isometric Convolution来建模这些局部特征间的关系，即全局关系。这里的Isometric Convolution其实就是卷积核等于序列长度的因果卷积。之后再使用同样kernel和步长的1D转置卷积（Conv1dTrans）进行上采样，将序列长度扩大i倍得到原始序列的长度。

对于每一层的输出Y^global,i_s,l，通过一个2D卷积将不同尺度的计算结果合并，这一步相当于融合多尺度信息，之后将输出送到FFN和Add&Norm模块，即得到该MIC层的输出y_l。对最后一层MIC的输出Y_s,N做一个线性映射和截取操作后得到季节项的未来预测序列Y_s。

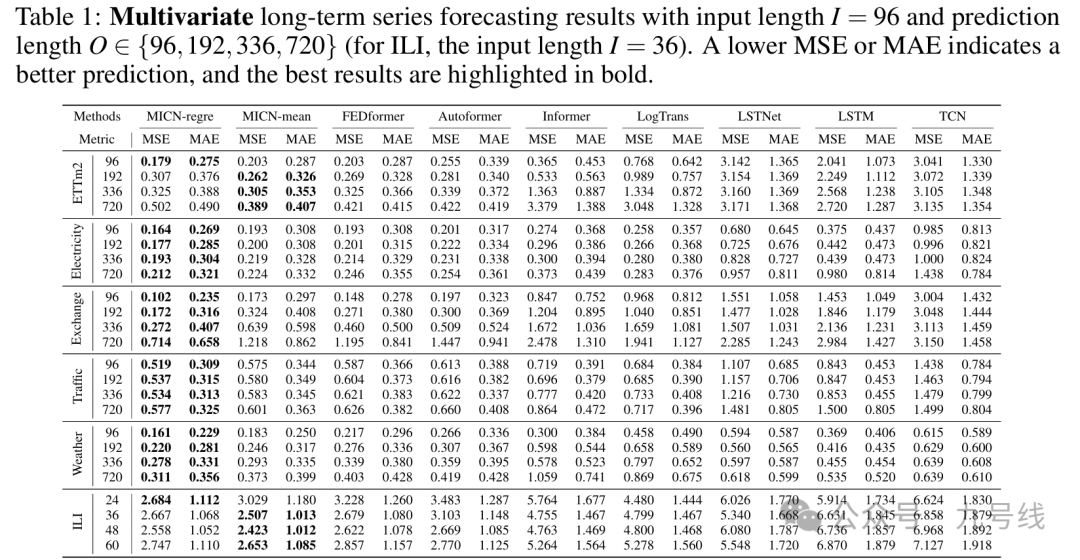
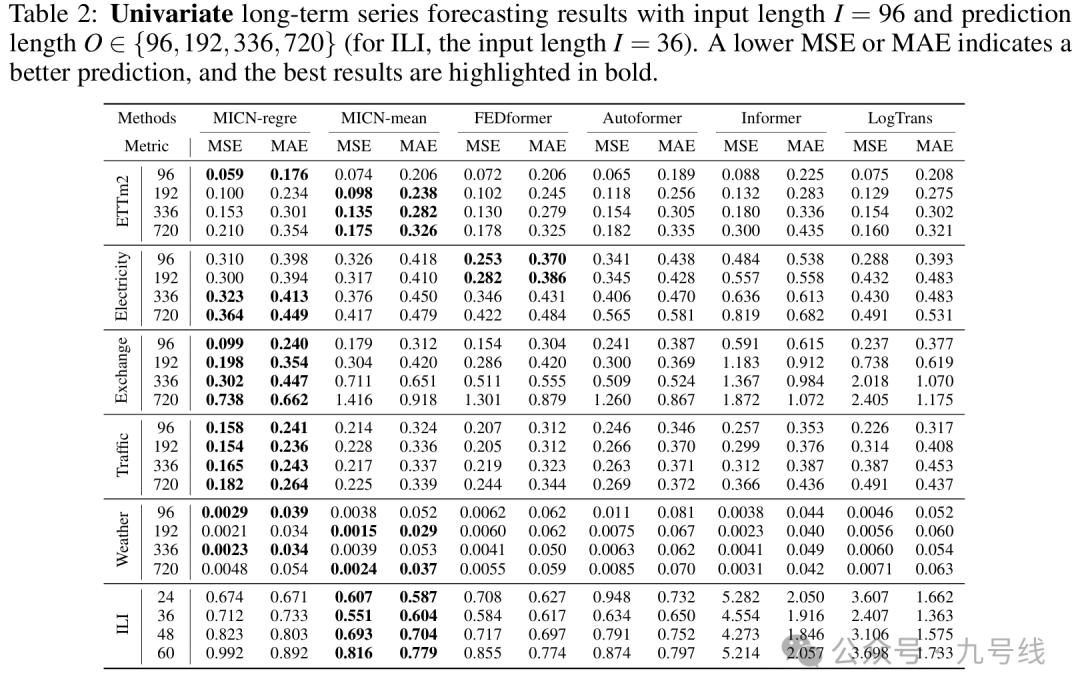
整体来说，MICN作为2023年提出的模型，其预测效果只能说比之前的传统TransFormer类模型略有增强。

四、基于GCN的时序预测模型

GCN在时序预测领域的应用主要跟LSTM结合以及MSGNet。MSGNet在之前的文章《基于二维神经网络模型的一维时序预测——TimesNet系列》中也提到过，发表于论文《MSGNet: Learning Multi-Scale Inter-Series Correlations for Multivariate Time Series Forecasting》，主要创新之处引入了GCN网络用于提取不同变量间的关系。

MSGNet在TimesNet基础上做了如下修改：首先在输入端对原始Input数据进行Embedding（加入了词编码、位置编码以及时间编码），并且把CNN卷积网络换成了图卷积网络（GCN），同时增加了多头注意力机制（MHA），整个模型的框架如下图所示，核心组件是ScaleGraphBlock。

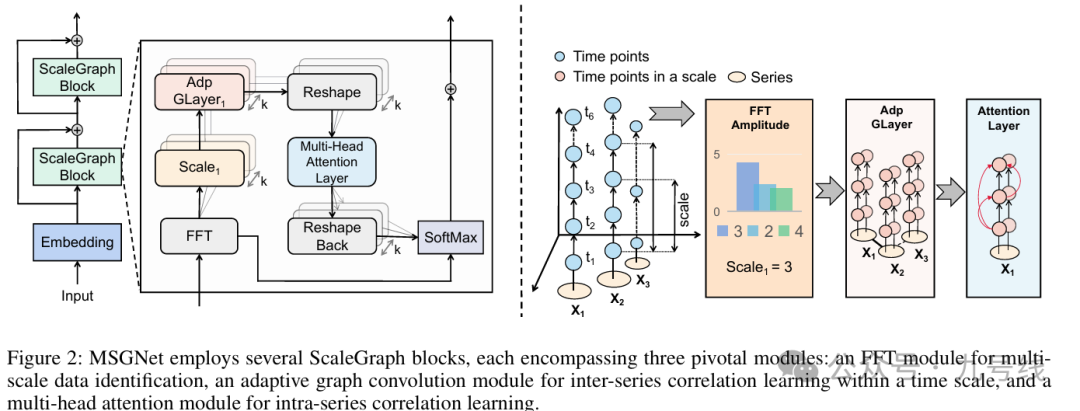
MSGNet的整个工作流程

1、首先对输入数据（MSGNet的输入数据是N*L，即时间长度为L的N个变量，N可以为1）进行Embedding，包括向量编码、位置编码和时间戳编码。

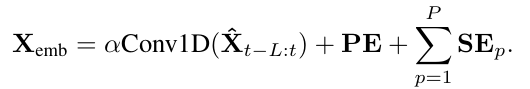
2、将编码后的数据X_emb输入FFT（快速傅里叶变换），提取原始时间序列中的不同周期划分形式，这步和TimesNet一样。通过FFT转换后提取振幅A前k大的周期序列，并将1D向量reshape为2D向量X^i，这里i属于（1，2，3...，k），即振幅第i大的周期序列；

3、将X^i输入图卷积模块，经过图卷积网络后输出H^i_out，这里W和E都是可学习的参数矩阵。

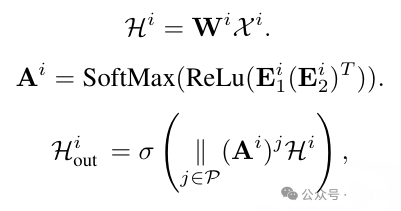
4、将H^i_out的形状由dim*si*fi重新reshape成N*si*fi，输出为X_hat^i，这里si*fi=T即原始序列长度。接着将X_hat^i输入多头注意力机制MHA，得到X_hat^i_out；

5、最后一步，通过Adaptive Aggregation将X_hat^i_out加权相加，权重为每个周期i对应的振幅，最后通过一个线性变换将dim*L转换为最初的形状N*T。

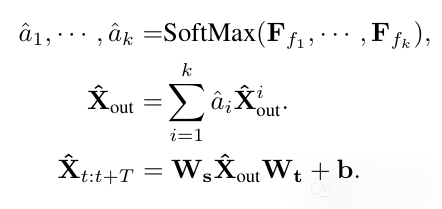
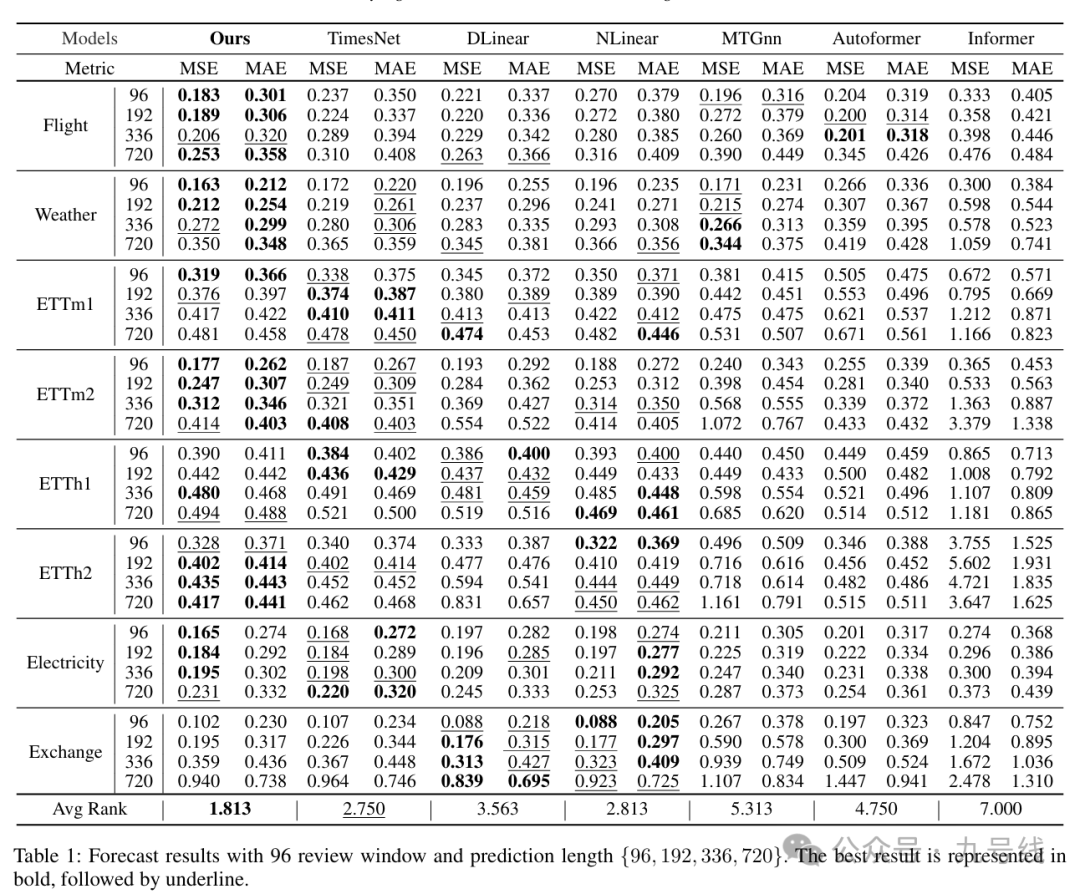
MSGNet在航班数据、天气预报、ETF、电力等数据集上的预测效果优于TimesNet、DLinear/NLinear、MTGnn、Autoformer、Informer等模型，但在金融时间序列Exchange上的预测效果不如DLinear/NLinear。

五、混合时序预测模型

为了充分利用各类基座模型的不同优势，比如CNN善于提取局部信息、Transformer善于捕捉全局依赖信息等，近些年开始出现一些将不同基座模型结合的时间序列预测模型，比如PERIODICITY DECOUPLING FRAMEWORK（PDF）和TimeMixer++。

1、PERIODICITY DECOUPLING FRAMEWORK

又是一篇ICLR论文，2024年来自清华大学的团队发表《PERIODICITY DECOUPLING FRAMEWORK FOR LONG TERM SERIES FORECASTING》，提出了PERIODICITY DECOUPLING FRAMEWORK（PDF）模型。PDF模型最大的创新之处是，把时间序列划分为多模态（不同频率）的基础上，每个模态下再进一步划分为长期趋势（Long-term）和短期趋势（Short-term），并分别使用Transformer和1DConv提取相应信息。

PDF的结构图如下，一共由3个核心模块组成。

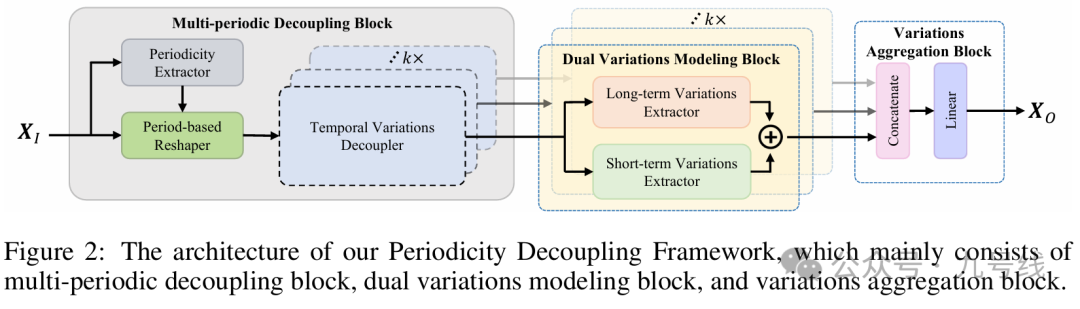
（1）Multi-periodic Decoupling Block

这一步类似TimesNet，将原始输入X_I（每次都是单变量输入，PDF模型不考虑变量间相关性，这也是它的一个问题）经过FFT（快速傅里叶变换），提取原始时间序列中的不同周期划分形式，但有别于TimesNet中的做法，此处作者认为不仅要考虑幅值强度最大的几个频率，还需要考虑频率取值最大的几个频率，因为前者反映了序列的主要组成部分，后者代表了序列的高频变化部分。

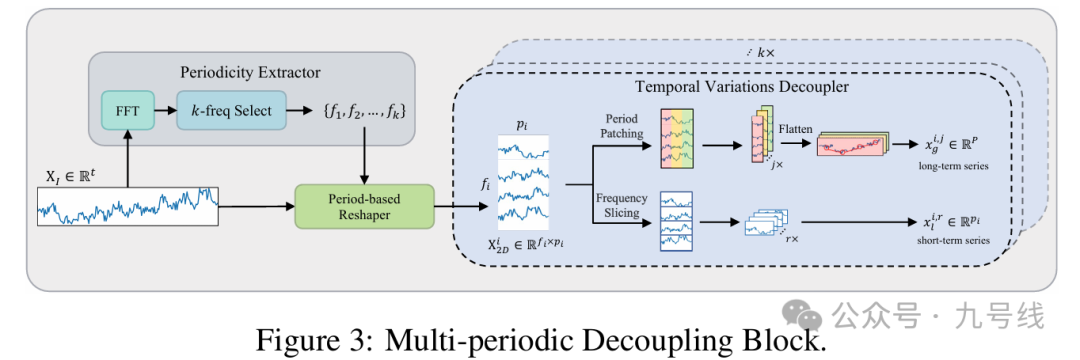
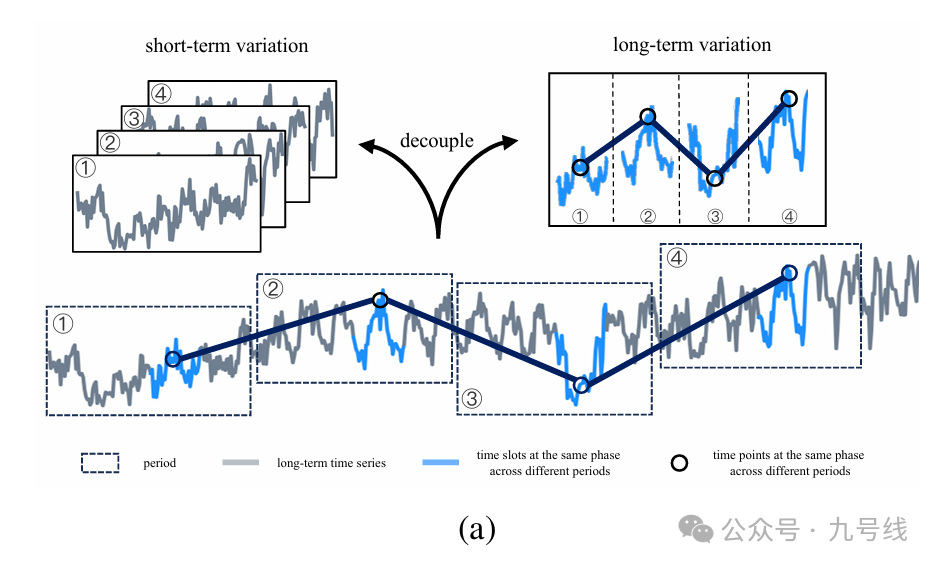
接着，将分解后得到的不同尺度时间序列X^i_2D∈R_fi*pi分解为长期趋势和短期趋势。对于长期趋势：以长度p步长s对每个period（一共fi个）进行切割，然后将所有period中表示相同阶段的切割块按顺序拼接起来，得到N=（pi-p）/S+1个长度P=fi*p的长期变化序列x^i,j_g；对于短期趋势：直接将X^i_2D的每一行序列单独视为短期变化序列，于是得到fi个长度为pi的短期变化序列x^i,r_l。

（2）k层Dual Variations Modeling Block

对于每个尺度上得到的长期变化序列x^i,j_g和短期变化序列x^i,r_l，分别利用Transformer和1D卷积来建模，将最后的结果X^i_g、X^i_l相加得到X^hat_i，具体操作如下图所示。

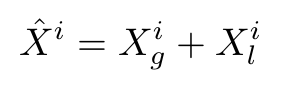
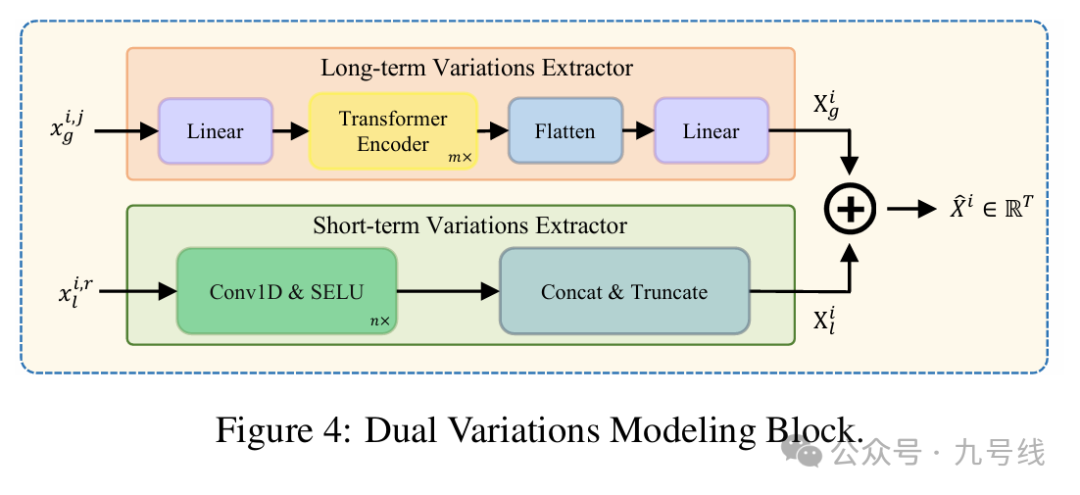
（3）Variations Aggregation Block

k个尺度对应做k次Multi-periodic Decoupling Block和Dual Variations Modeling Block操作，得到k个X^hat_i，经过Variations Aggregation Block拼接并线性映射后得到最终的输出X_o。

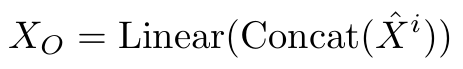
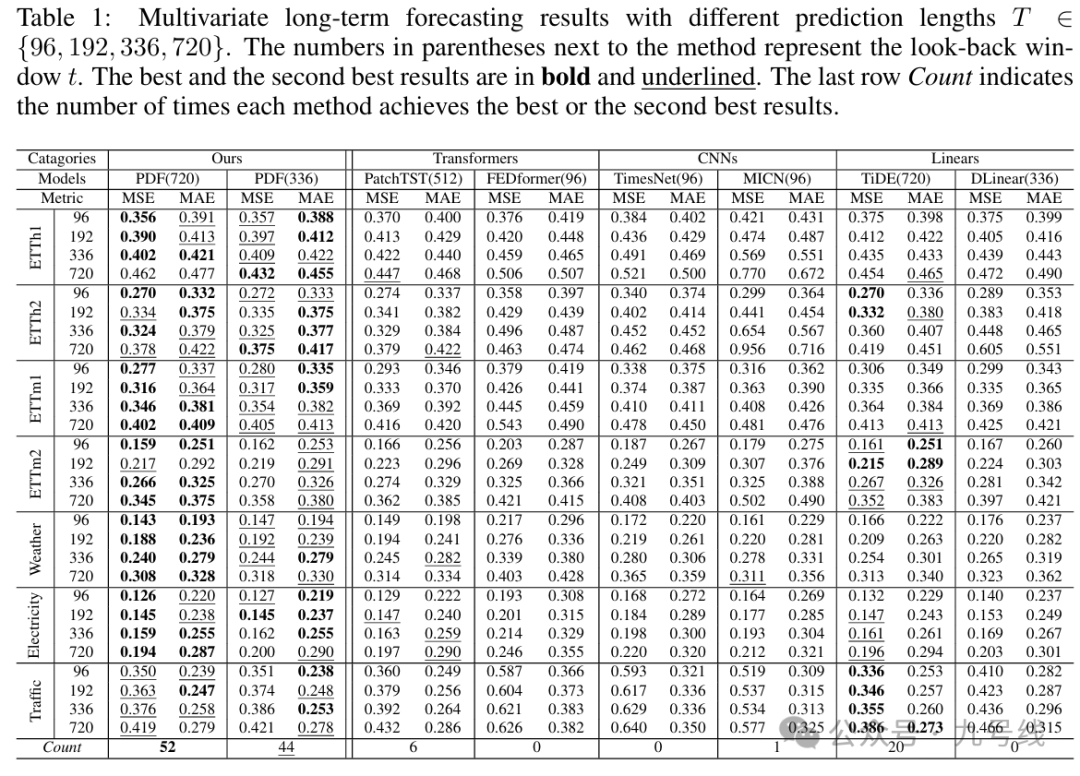
PDF本质是个单变量预测模型（每次输入一个变量序列），回看周期t取720和336两种情况，预测结果以及和其他模型的比较见下图：

2、TimeMixer++

ICLR2025的高分oral文章《TimeMixer++：A General Time Series Pattern Machine for Universal Predictive Analysis》，来自MIT、港科大、浙大以及格里菲斯大学的华人团队联合推出了一种全新的深度模型架构TimeMixer++。TimeMixer++在长时序预测、短时序预测、时序分类、异常检测等8项时序任务上的效能全面超越了Transformer等模型，实现了通用的时间序列建模和应用。

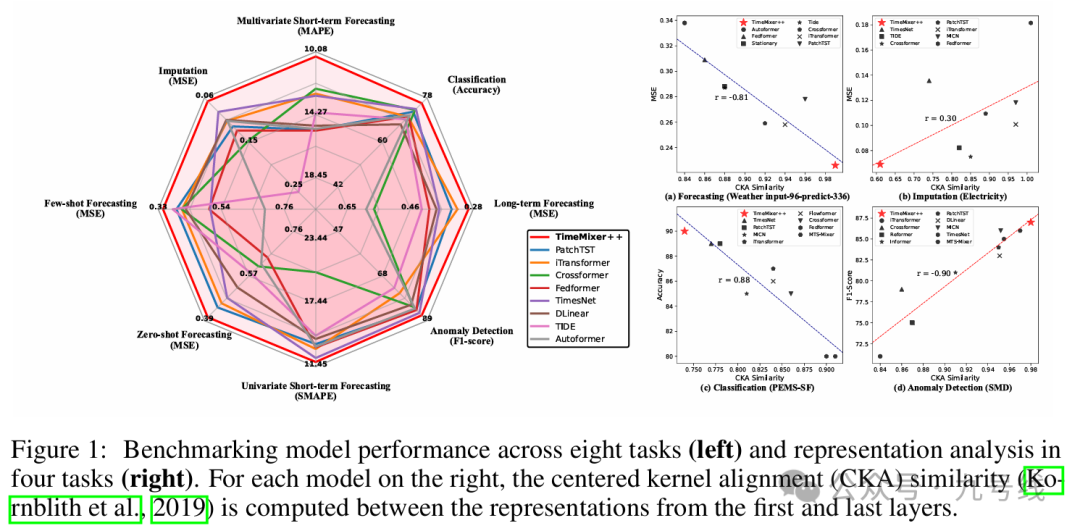
TimeMixer++可以理解为TimeMixer的升级版，TimeMixer是做时序预测任务的，而TimeMixer++是做通用时序任务的。此外两者最大区别在于周期项（ seasonal components）和趋势项（trend components ）的提取方式，TimeMixer用移动平均提取趋势项，而TimeMixer++采用了轴向注意力（axis-specific attention）来分别建模周期和趋势。

TimeMixer++的结构图如下，一共由5个核心模块组成，其中a模块用来做下采样，b、c、d、e模块共同构成了MixerBlock模块。

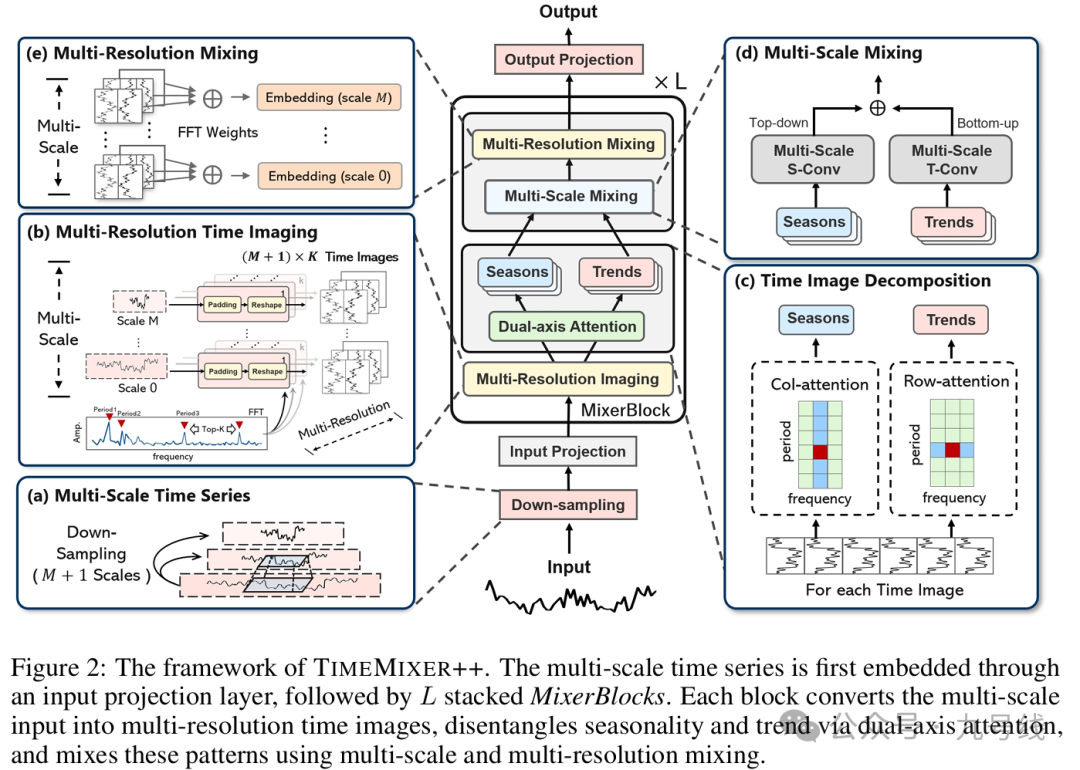
（a）Multi-scale Time Series

下采样模块，类似TimeMixer，将原始输入序列x∈R_p*c转换为不同周期尺度的子序列x_m∈R_[T/2^m]*c。此处T是原始序列长度、c是变量个数，m表示第m个尺度。比如m=0的时候，x_0就是原始序列。

值得注意的是，在输入MixerBlock模块前，通过input_projection对最粗粒度的序列x_M进行了一个自注意力操作，用于获取多通道间的相关信息，作者认为最底（M）层的粗颗粒度序列保留了大量全局信息。

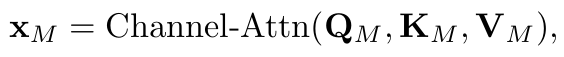
然后对所有的x_0...x_m...x_M进行一个嵌入操作，将x_m∈R_[T/2^m]*c映射为x_m∈R_[T/2^m]*d。

（b）Multi-Resolution Time Imaging

类似TimeMixer，将所有尺度的序列都按照FFT变换后，reshape为pk*fk的二维表现形式，由于要对每个尺度的序列都提取幅度最大的前k个频率，所以fk=[T/2^m]/pk。这里z^(l，k)_m∈R_pk*fk*d表示第l层、第m个尺度下的第k个频率对应的二维向量。

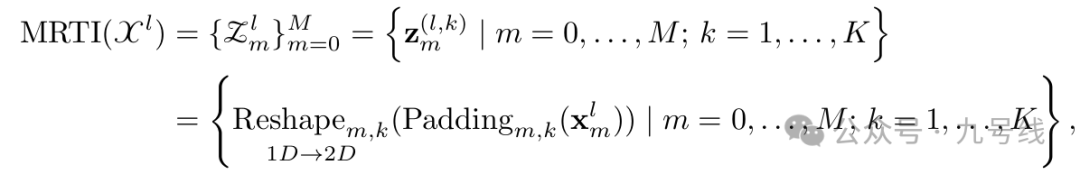
（c）Time Image Decomposition

z^(l，k)_m∈R_pk*fk*d的每一行代表不同周期内的同一时间点（可以视为趋势），每一列代表频率fk下的某一完整序列（可以视为周期），类似前面PDF中的概念，再贴一下这张图。

因此这里采用轴向注意力来分别建模趋势（row）和周期（column）。具体来看，就是对行采用attention得到趋势分量，对列采用attention得到周期分量。

（d）Multi-scale Mixing

同样类似TimeMixer，将来自不同尺度m的趋势项和周期项信息融合。但因为是2D图像，不能直接线性相加，而是采用图像领域中常用的上下采样操作（下采样用2D卷积，上采样用2D transposed卷积）来对齐不同尺度。

这里趋势和周期项的融合方式也和TimeMixer一样，对于周期项按自下而上（bottom-up）的方式进行信息融合、对于趋势项按自上而下（top-down）的方式进行信息融合。

最后将每个尺度下的第k个频率对应的周期项和趋势项相加并重新reshape为一维向量，得到z^(l，k)_m∈R_pk*fk*d。

（e）Multi-resolution Mixing

将尺度m下的所有频率对应的z^(l，k)_m按振幅加权相加，得到第l层下m尺度对应的向量x^l_m

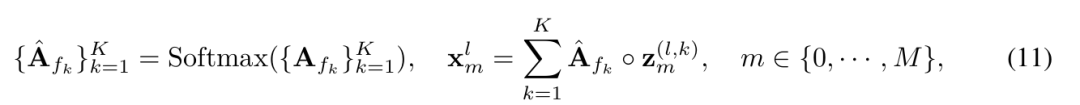
在最后一步的Output Projection，将经过第L层的x^L_m聚合，得到最终的输出，m个尺度对应m个head。

TimeMixer++本质上是一个融合了之前模型所有优点（原始序列分解、不同变量间的信息融合、局部和全局信息提取）的合成模型，因此其在长短期预测、插补、分类、异常检测等任务上相较TimeMixer均有更优异的性能，相较传统模型性能领先更多。例如在长期预测中，相比 iTransformer 在 Electricity 数据集上 MSE 降低 7.3%，MAE 降低 6.3%。

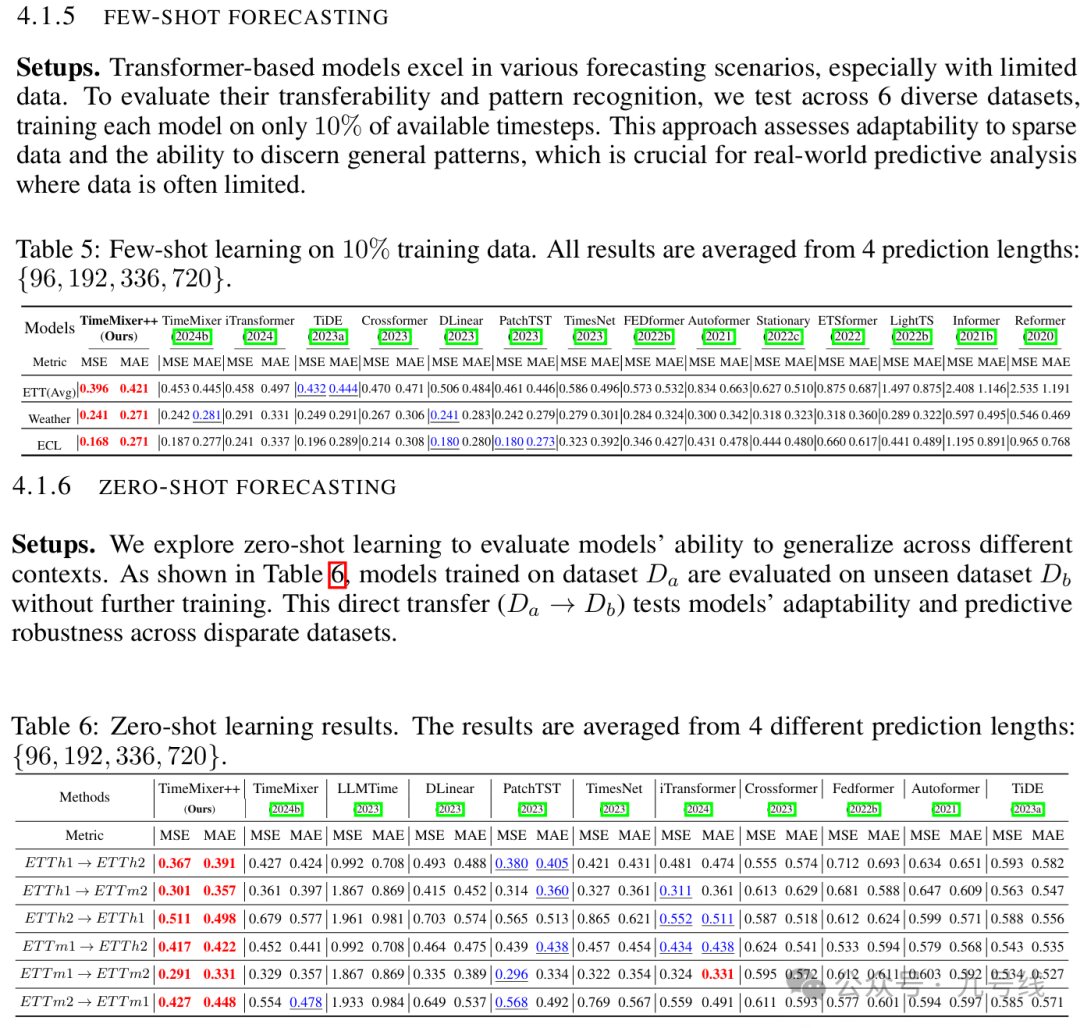
更重要的是，TimeMixer++在少样本（FEW-SHOT）和零样本（ZERO-SHOT）预测任务中表现出色，展现了良好的模式识别和泛化能力。

————————————华丽的分隔符————————————

能坚持读到这里的小伙伴不容易，发个福利，后台私信发送上述所有涉及论文的PDF文件。下面在国内金融市场做一些应用测试，比如指数收益率、波动率预测等等。

这里给大家推荐一个很好用的做时间序列建模的python开源库——Time-Series-Library（https://gitcode.com/GitHub_Trending/ti/Time-Series-Library/tree/main）。该开源库由THUML团队开发，旨在帮助开发人员快速进行时间序列数据的预处理、建模与评估，它集成了多种深度学习时间序列预测模型，上文提到的以及没提到的各种模型都由涉及，除了TimeMixer++（官方尚未提供代码）。

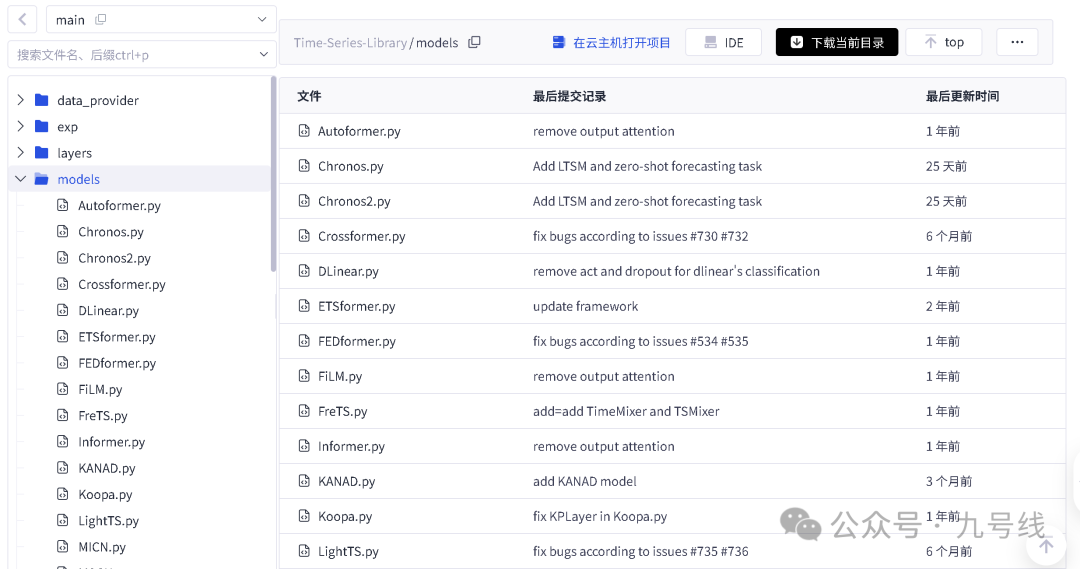
考虑到TimesNet因为引入了两层Inception模块运行速度实在太慢暂不测试，TimeMixer++官方尚未提供代码也无法测试，下文测试主要用到TimeMixer、DLinear、iTransformer、PatchTST、MSGNet等几个模型的预测效果。

所有模型均使用并共享默认参数，回看步长取60、预测步长取5，预测标的为股票（不同风格）、债券（利率和信用）、商品（黄金、铜、铝）的日收盘价序列，做了NonStationary——>Stationary处理。起始日期为2010/1/1，样本外预测区间为2021~2025，即每年初利用滚动扩展窗口的数据训练模型，固定参数后再预测当年的数据。预测结果如下：

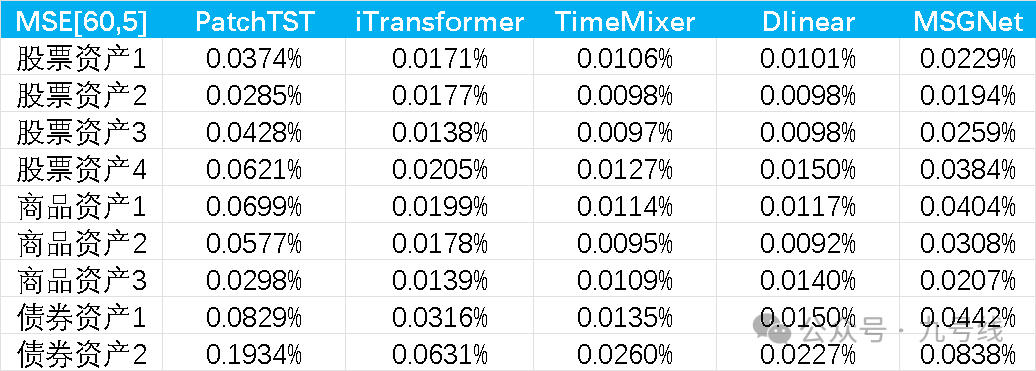
可以看到iTransformer、TimeMixer、DLinear的样本外预测效果非常好。PatchTST的参数patch和stride长度会对预测效果有比较大的影响，原论文的回看步长为512、预测步长最小为96，所以设置patch=16、stride=8，因此可能并不适用我这里做短期预测。MSGNet的训练时间最长，预测效果介于PatchTST和DLinear、TimeMixer之间。

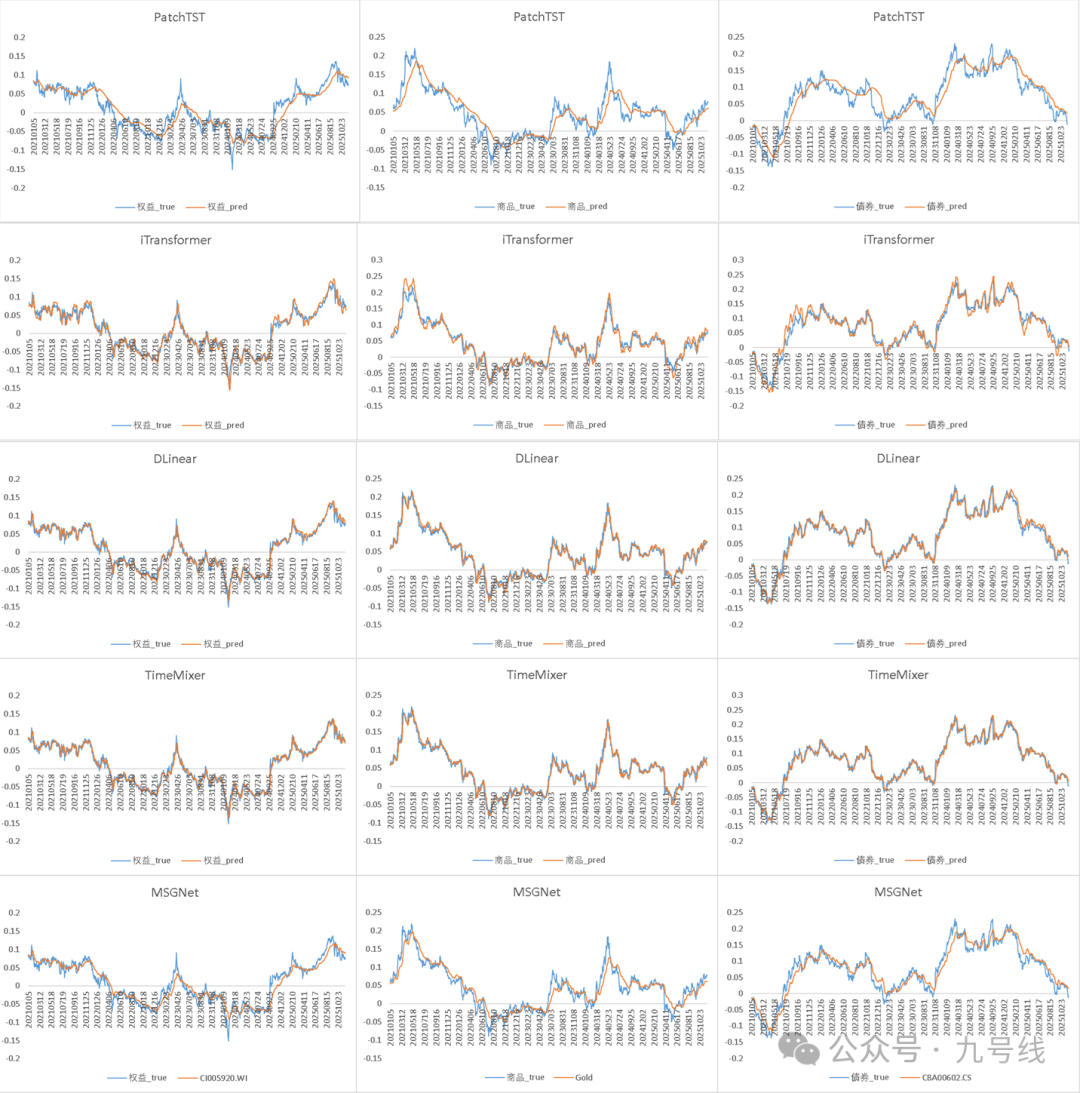
下面再展示下样本外（2021~202511）预测效果，可能是分辨率的关系，DLinear、TimeMixerd以及iTransformer的预测图看着非常精确，其实放大了看误差还是挺大的。