磐松观点｜股票的风格贝塔

作者：磐松资产

题图：磐松资产微信公众号

概要

贝塔衡量了股票收益对风格因子收益的敏感程度，它反映了股票的系统性风险。本文首先介绍了贝塔的定义和估计方法，其次展示了不同风格贝塔的特点与分布，最后介绍在投资组合构建过程中，如何通过控制风格贝塔的偏离来降低拥挤交易的风险。

贝塔的定义和估计方法

贝塔衡量了单一资产的系统性风险暴露。Sharpe（1964）的资本资产定价模型（Capital Asset Pricing Model, CAPM）首次提出用单一的股票市场因子（MKT）解释资产收益 [1] ；在此基础上，Fama and French（1993）提出三因子资产定价模型，引入小盘股因子（SMB）和价值因子（HML）[2, 3] 。对于某时刻 t 的股票 i ，Fama-French 三因子模型的资产定价公式如下所示：

后续也有许多学者对三因子模型进行扩展，并且提出更多的风格因子，以增强模型对股票回报的解释能力，例如 Carhart (1997) 提出的动量风格 [4] ，以及 Fama and French (2015) 提出的盈利、投资风格 [5] 等等。这些由多个不同的风格因子构成的资产定价模型统称为多因子模型，而多因子模型中的贝塔衡量了股票在不同因子上的风险暴露。

磐松当前的投资过程关注了六种风格贝塔。其中，每种风格因子对应一种投资策略：

1. 股市：股票市场相对短期无风险利率的超额回报。

2. 债市：利率债市场相对短期无风险利率的超额回报。

3. 小盘股：小盘股相对大盘股的超额回报。在中国A股市场，小盘股历史上具有显著的超额收益。

4. 价值：价值股相对成长股的超额回报。价值风格（详见往期《磐松观点｜A股价值投资》）倾向于投资那些当前市场价格低于其内在价值的公司。

5. 质量：基本面质量较优的股票相对较差的股票的超额回报。质量风格关注上市公司的财务信息，倾向于投资稳定、高盈利能力的股票。

6. 动量：过去一段时间收益高的股票相对收益低的股票的超额回报。动量风格认为股票过去的涨跌趋势会在未来延续。

💡 为什么要衡量股票的债市贝塔？

是出于以下两点考虑：
（1）我们用于研究和估计风险的样本总体上呈现出利率下行的长期趋势。当前国内处在低利率环境，如果不控制债市贝塔，投资组合可能会有债市敞口，从而受到未来加息的负面影响。
（2）低波动、高股息的股票策略会周期性地获得投资者的青睐，这些股票往往具有高债市贝塔，控制投资组合在债市贝塔上的偏离，有助于规避与低波动、高股息策略相关的拥挤交易。

💡 价值风格和质量风格有什么关系？

价值风格倾向于投资那些以低估值交易的公司；质量风格倾向于投资那些因为稳定的高盈利能力而理应获得高估值的公司。从历史表现看，质量风格能够创造正向的超额收益 [6] ，尤其当与价值风格结合、买入估值合理的高质量股票时表现更优。

基于上述6种风格因子，对应的资产定价公式如下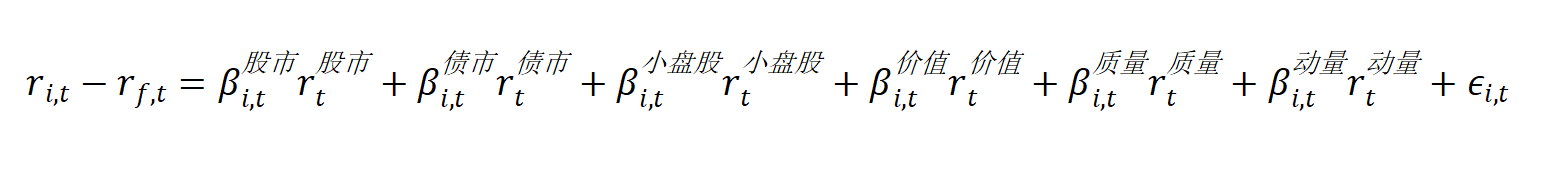：学术界通常采用（滑动窗口）时间序列回归的方式进行风格贝塔估计 [7] ，但对于个股而言，时序回归的样本数量有限，纯粹依靠历史数据回归得到的风格贝塔具有较大的测量误差。为了解决这个问题，我们在估计风格贝塔时采用贝叶斯收缩的方法 [8] ，使风格贝塔向目标均值靠拢，以减少基于历史数据的回归估计中的噪声。

贝塔的特点和分布

股票的风格贝塔具有明显的时变性。例如，上市公司因技术革新，成长属性变强，驱动估值重构，其价值贝塔可能会由正转负；当公司经营质量向好，推动市值持续扩张时，其小盘股贝塔可能逐渐衰减甚至转负。

下图展示了2025年7月底全市场股票风格贝塔的直方图分布情况。可以看到，股市贝塔大致以 1 为中轴线对称分布；因为小盘股数量多，但市值小，所以小盘股贝塔大多分布在零轴的右侧；价值贝塔和市值总体上呈正相关，故价值贝塔存在一定的左偏；质量贝塔、动量贝塔和债市贝塔都基本围绕零轴对称分布。

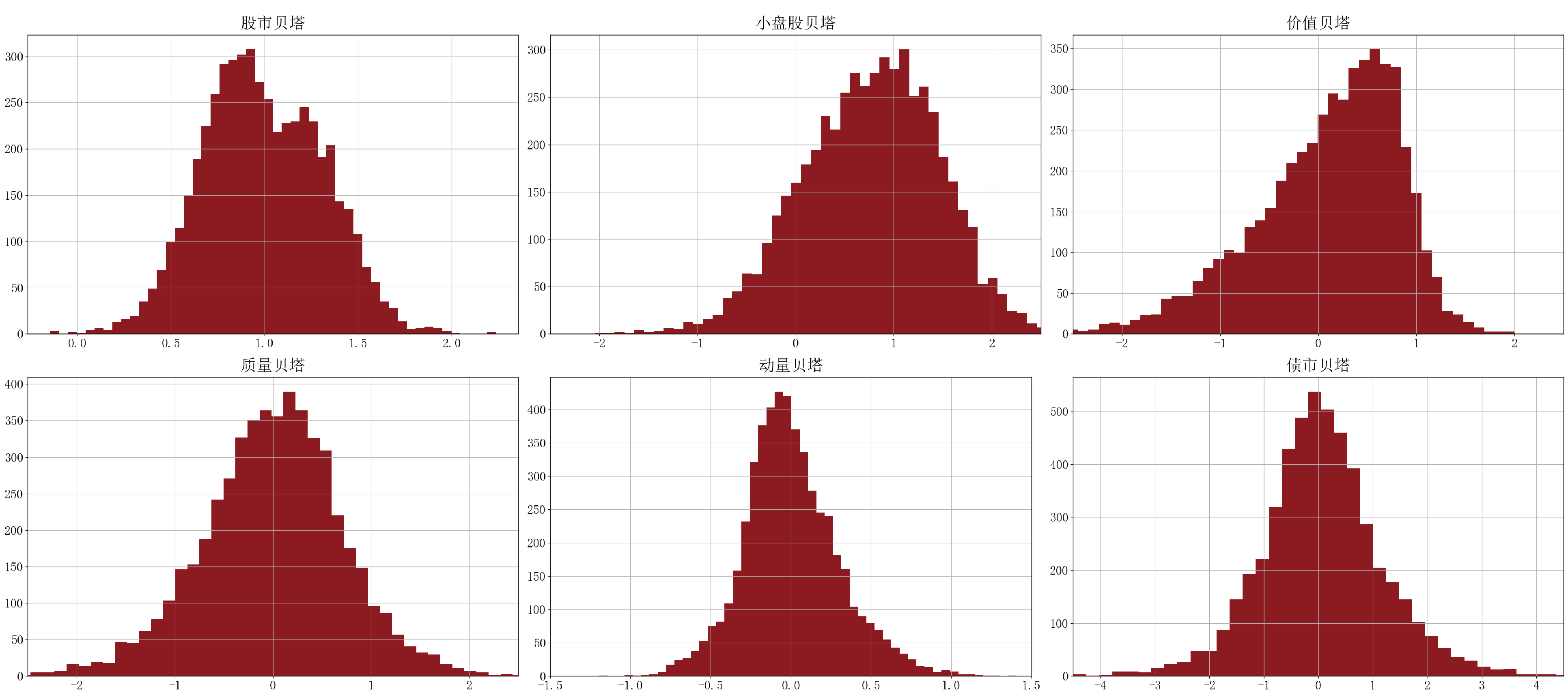
图1 股票风格贝塔直方图分布

投资逻辑上，股市贝塔和债市贝塔具有天然的负相关性。例如，防御型行业的需求弹性小，其回报随市场经济周期整体变动的波动较小，因而具有较小的股市贝塔；同时，防御型行业的股票具有稳定的现金流和分红，和债券具有类似的投资属性，因而债市贝塔显著为正。对于顺周期行业，其股价变动与经济周期高度同步，因而具有较大的股市贝塔；同时，顺周期行业的盈利波动较大，有更低的利率敏感性，因而债市贝塔较小。

下图为2015年至今不同行业的股市贝塔与债市贝塔散点图，可以看到二者整体呈现负相关趋势。其中公共事业行业为典型的防御型行业，具有最低的股市贝塔和最高的债市贝塔；而中国的房地产行业为顺周期行业，因而具有最高的股市贝塔和较低的债市贝塔。

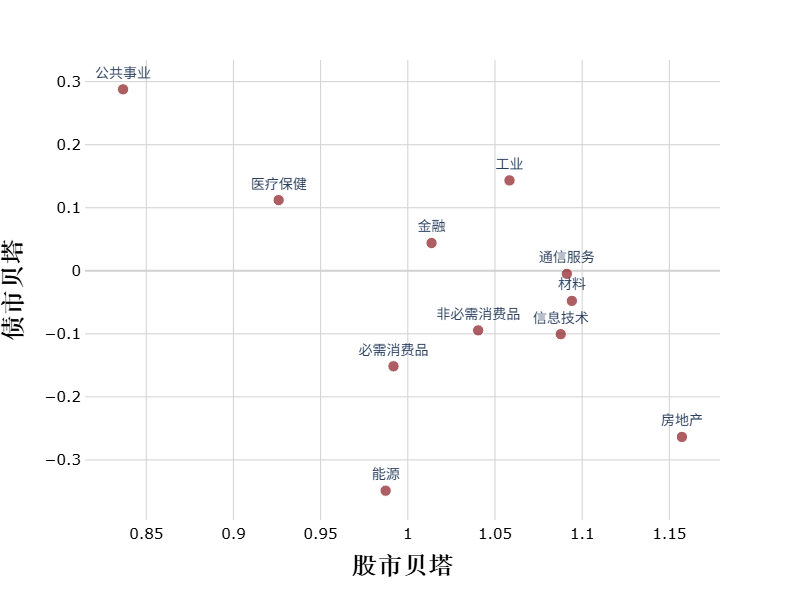
图2 不同行业的股市贝塔和债市贝塔

基于上文对贝塔分布特征的系统性描述，我们进一步聚焦于三个典型案例（数据选取自2025年7月底）：

01 贵州茅台（典型的蓝筹股）

股市贝塔接近 1，说明长期来看，该股票的回报和整体股票市场基本保持一致；茅台是超级大盘股，具有较负的小盘股贝塔；茅台所属的白酒板块为顺周期行业，具有负的债市贝塔；茅台还是具有稳定且较高盈利的优质股，质量贝塔显著为正。

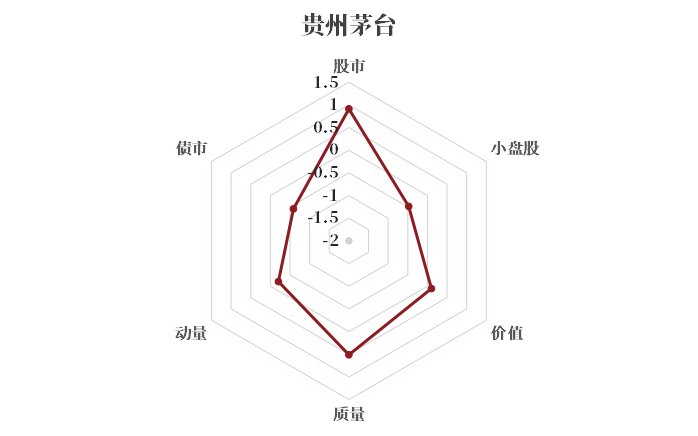
图3 贵州茅台各风格贝塔分布图

02 长江电力（典型的高股息股票）

该公司有较高的股息率和派息率，持续的股利发放使得股票持有人享受到稳定的现金流（类似债券发放利息），因而该公司也拥有很高的债市贝塔。

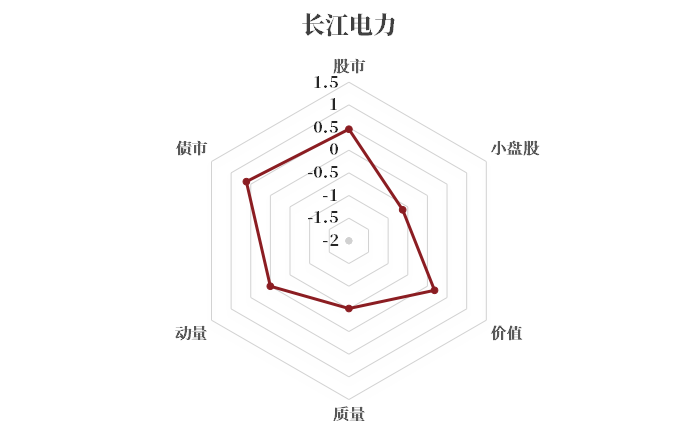
图4 长江电力各风格贝塔分布图

03 特征 v.s. 贝塔

值得一提的是，股票的风格特征和风格贝塔有时是相互背离的。例如，有的小（大）盘股股票可能具有负（正）的小盘股贝塔，说明该股票的回报与小盘股因子的回报负（正）相关。下面展示两个小盘股贝塔与股票的市值特征相背离的例子，左图的小盘股福光股份具有负的小盘股贝塔；右图的大盘股美的集团，反而具有正的小盘股贝塔。

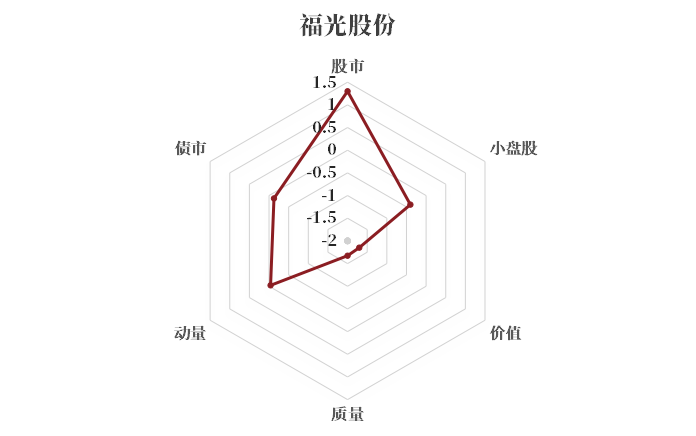
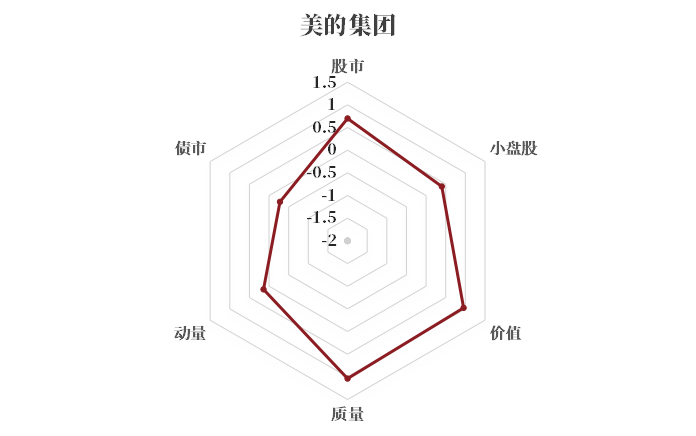
图5 福光股份和美的集团的风格贝塔分布图

控制投资组合风格偏离

回顾往期《磐松观点｜投资组合，灵活智造》，磐松的投资过程，不仅最大化超额收益、控制投资组合的风险与交易成本，还严格控制了投资组合的风格偏离，从而规避参与拥挤风格的投机行为。在优化器的效用函数中，我们将风格偏离单独作为一个惩罚项，让最优投资组合具有尽可能少的风格暴露。

💡为什么要施加额外的风格偏离惩罚，而不是在风险模型中将风格贝塔作为风险因子？

磐松自研的风险模型涵盖广泛的风险因子（包括风格贝塔），但是风险模型对所有风险因子一视同仁；而特定的风险因子既受投资者格外关注，其周期性表现又超出基金管理人的预测能力范畴，所以需要施加额外惩罚。
根据历史经验，我们识别出上文所述的六类风险源符合特定标准。这些风格因子被大量投资者视为同质化的超额收益来源。更重要的是，它们可能周期性陷入“拥挤交易”状态，即不同的管理人同时在它们上面有相似的暴露，例如2024年春节前大量管理人在小盘股因子上有正暴露。
当很多管理人具有相似的风格偏离时，会使得风格因子拥挤。造成的后果是，一方面风格因子收益降低，波动加剧 [9] ，风险模型难以有效预测；另一方面，不同管理人的投资收益被动地高度相关，投资者无法通过分散投资管理人来降低整体组合风险。

风格偏离惩罚项具体指的是每个产品投资组合的各风格贝塔相对其业绩基准的偏移程度。计算公式为：

举一个直观的例子，假设一个基金产品对标的业绩基准是小（大）盘股指数，具有较高（低）的小盘股贝塔。为了使风格偏离惩罚项尽可能接近于零，最优投资组合会倾向于配置小（大）盘股。

值得注意的是，风格偏离惩罚聚焦于风格贝塔（如价值贝塔）的暴露，而非风格特征（如股息率）。举个具体的例子，一个投资组合可能在超配价值股（风格特征）的同时，保持了价值贝塔偏离约等于零；换言之，即便投资组合的估值看似便宜，也不一定会在价值风格失效期持续跑输。

风格拥挤虽然是风险源，但亦可成为风险可控的战术机会。随着“聪明贝塔”类产品的普及，非专业投资者追逐风格的交易行为可能会加剧风格收益波动。一方面，我们可以在股票回报预测模型中研发相关的信号，通过战术风格轮动追求收益；另一方面，通过优化器对风格暴露施加惩罚，我们又能确保风格偏离的长期均值为零。

总结

本文描述了A股市场上6种不同的风格贝塔，结合具体案例分析了风格贝塔的属性及彼此的联系，并展示了控制风格偏离在构建投资组合中的应用。

股票的风格贝塔不仅被直接应用在效用函数的风格偏离惩罚项中，还作为系统性风险因子被应用在风险模型中。我们后续将发布更多的白皮书介绍风险模型，敬请期待！

参考文献

[1] Sharpe, W. F. (1964). Capital Asset Prices: A Theory of Market Equilibrium under Conditions of Risk. The Journal of Finance, 19(3), 425.

[2] Fama, E. F. , & French, K. R. . (1993). Common risk factors in the returns on stocks and bonds. Journal of Financial Economics, 33(1), 3-56.

[3] Fama, E. F. , & French, K. R. . (1996). Multifactor explanation of asset pricing anomalies. Journal of Finance, 51(1), 55-84.

[4] Carhart, M. M. (1997b). On Persistence in Mutual Fund Performance. The Journal of Finance, 52(1), 57–82.

[5] Fama, E. F. , & French, K. R. . (2014). A five-factor asset pricing model. Journal of Financial Economics, 116(1), 1–22.

[6] Novy-Marx, R. (2013). The other side of value: The gross profitability premium. Journal of Financial Economics, 108(1), 1 – 28.

[7] Ang, A., & Kristensen, D. (2012). Testing conditional factor models. Journal of Financial Economics, 106(1), 132–156.

[8] Vasicek, O. A. (1973). A Note on Using Cross-Sectional Information in Bayesian Estimation of Security Betas. The Journal of Finance, 28(5), 1233–1239.

[9] Brown, G. W., Howard, P., & Lundblad, C. T. (2021). Crowded Trades and Tail Risk. Review of Financial Studies, 35(7), 3231–3271.

*重要声明

风险提示：本内容刊登于此仅出于传递信息之目的，不构成投资建议，其内容是基于我们认为可靠且已公开的信息，但我们对这些信息的准确性及完整性不做任何保证，也不保证文中观点或陈述不会发生任何变更；在不同时期，可发出与这些信息所载资料、意见及推测不一致的内容。

版权提示：如转载使用，请注明来源及作者、文内保留标题原题以及文章内容完整性，并自负版权等法律责任。

往期推荐：

磐松观点｜解析股票交易成本

磐松观点｜A股价值投资

*点击【官网】进入磐松官方网站或【联系我们】获取更多信息。