如何基于个股股价跳跃行为做择时？

作者：招商定量任瞳团队

题图：招商定量任瞳团队 微信公众号

本报告研究了股价跳跃在指数择时上的应用。我们首先构建了跳跃不平衡指标，进一步创新性的将跳跃不平衡指标区分为隐含不平衡指标与暴露不平衡指标，验证了这些指标对市场收益预测的有效性。本报告的核心结论如下：

• 跳跃不平衡指标衡量了股票价格向上跳跃与向下跳跃的力量差。使用跳跃数量不平衡指标∆JDTNJ指标进行择时有一定效果。策略年化收益6.23%，夏普比为0.57，盈亏比1.46，年化超额为4.48%，夏普比为0.34。
• 我们将受市场跳跃影响的个股跳跃称之为暴露跳跃，它反映了那些受市场跳跃影响的个股的跳跃信息。这种跳跃信息更多地反映了市场参与者对市场整体波动的反应和情绪；将不受市场跳跃影响的个股跳跃称之为隐含跳跃，它反映了那些不受市场跳跃影响的个股的跳跃信息。这种跳跃信息可能包含了市场参与者对个股未来表现的预期或知情交易的概率，是个股交易的“隐含信息”。
• 使用隐含跳跃幅度不平衡指标∆JRTIJ进行择时具有较好的效果。策略共开仓33次，胜率60.87%。策略年化收益9.93%，夏普比为0.82，卡玛比为0.75，盈亏比达到2以上；年化超额为8.46%，夏普比为0.77，卡玛比为1.12。整体择时效果相比指标具有较为明显的提升。
• 我们以个股当月的隐含跳跃不平衡指标取标准差来代表市场的跳跃不平衡离散度JR_StdtIJ。将其与∆JRTIJ指标复合使用，复合指标择时策略年化收益为16.5%，年化超额收益15.49%，夏普比率为1.28，卡玛比率为2.41。
• 基于跳跃不平衡的择时策略信号，对富国上证综指ETF进行择时的策略效果整体较为稳健。策略年化收益为12.10%，夏普比率为0.89，卡玛比为1.49，策略年化超额收益9.78%，最大回撤仅为6.32%，夏普比1.14，卡玛比为1.55。
• 使用∆JRTIJ对国证成长指数进行择时同样具有较好的效果。正向策略共开仓34次，胜率64.71%。策略年化收益12.94%，夏普比为0.75，卡玛比为0.69，盈亏比为1.43；负向策略共开仓35次，胜率60%，年化收益为-9.92%，盈亏比为1.36。

*风险提示：本报告结果通过历史数据统计、建模和测算完成，在政策、市场环境发生变化时模型存在失效的风险；本报告所提及个股或基金仅表示与相关主题有一定关联性，不构成任何投资建议。

I 引言

在先前的研究《如何识别股价跳跃》中，我们探讨了股价跳跃在预测股票未来收益中的作用。通过使用分钟级数据识别A股市场上的股价跳跃，我们区分了正向跳跃与负向跳跃、隔夜跳跃与日内跳跃，并结合换手率，验证了跳跃因子在回报预测中的有效性，聚焦股票收益对自身股价跳跃的反应。

上一篇报告《基于股价跳跃关联的选股策略》中，我们基于股价的跳跃行为，提出了一个跳跃关联度指标，用来度量股票之间的关联程度，并在此基础上构建了点度中心性因子和跳跃关联动量因子。在这个报告中，我们主要关注股价跳跃在股票关联性方面的作用。

前两个报告中，我们均是从股价的跳跃出发，研究股价跳跃对个股未来收益的预测作用。在前面的研究中，我们发现了股价的跳跃对个股未来收益是具有较为显著的预测作用的，且股票之间的跳跃行为往往不是独立的，是具有相关性的。那么，自然而然我们就想到了是否能够应用股票的跳跃行为去对指数的涨跌进行预测。本篇报告是前两个报告的进一步延续，我们研究股价跳跃在指数择时上的应用。我们首先构建了跳跃不平衡指标，进一步创新性的将跳跃不平衡指标区分为隐含不平衡指标与暴露不平衡指标，验证了这些指标对市场收益预测的有效性。

II 跳跃不平衡指标构建

2.1 股价跳跃的识别

我们使用与报告《如何识别股价的跳跃》一致的方法来进行股价跳跃的识别，这里我们简单回顾一下。我们使用Jiang and Oomen(2008)的跳跃统计量来检验跳跃：

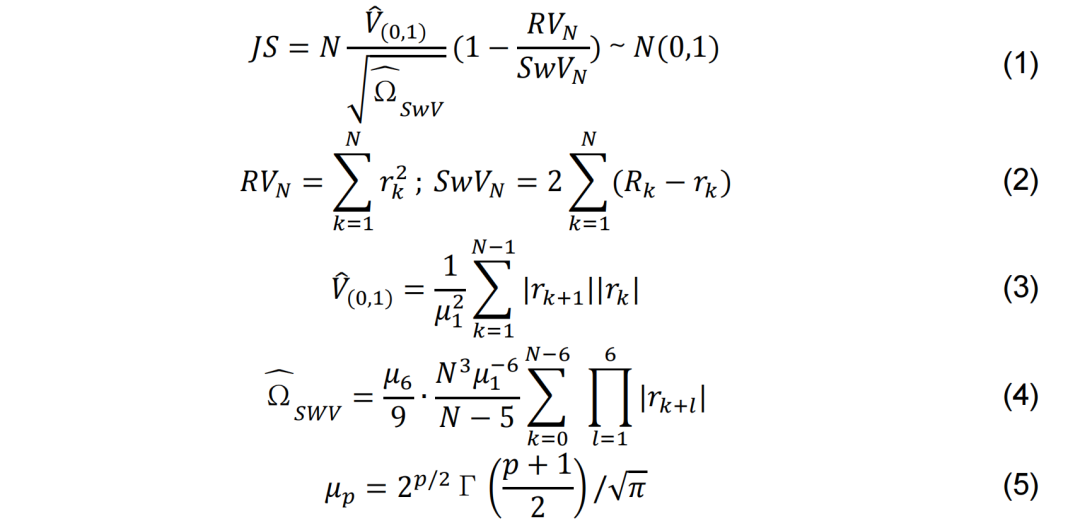
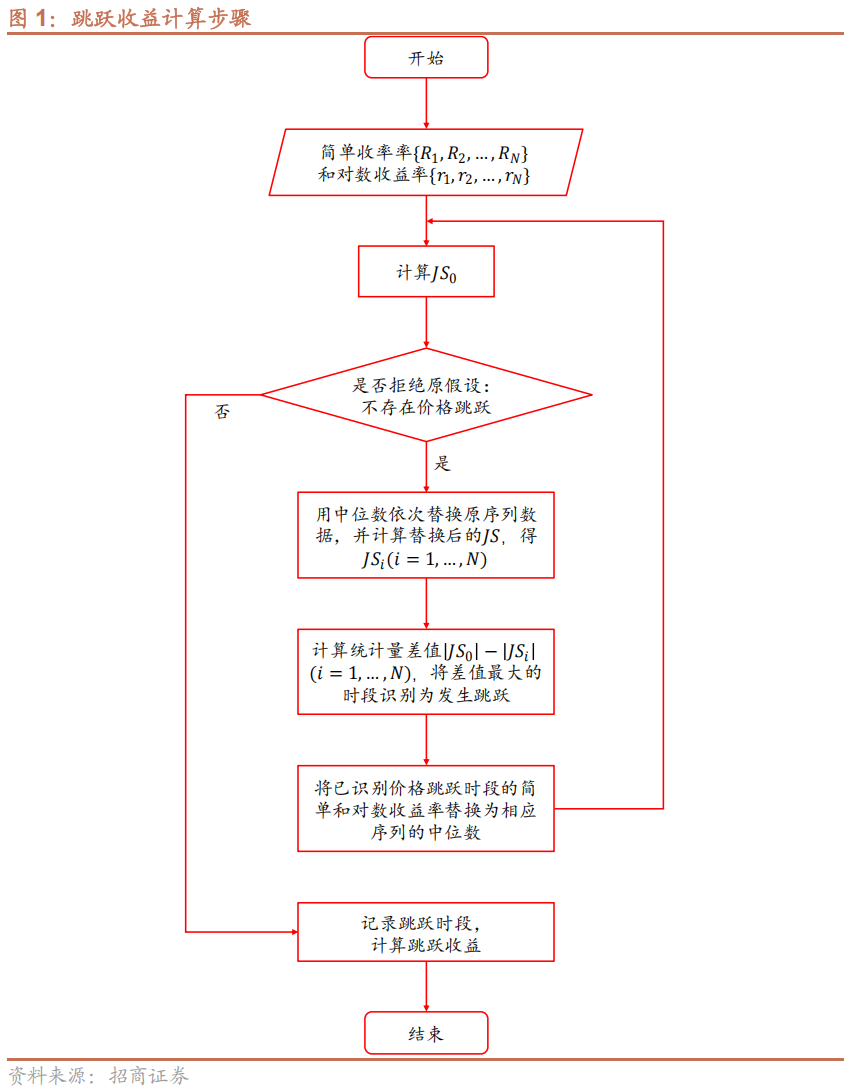
图1中我们画出了股价跳跃识别计算的步骤，计算步骤如下：

步骤一，对初始收益率序列计算跳跃检验统计量_JS0。若不拒绝原假设：不存在价格跳跃，则当日跳跃收益为0并结束检验；若拒绝原假设，则记录_JS0进行步骤二。

步骤二，将初始简单和对数收益率序列中每个值依次替换为相应序列的中位数，并基于替换后序列计算跳跃检验统计量，则可得_JSi(i=1,...,N)。

步骤三，计算统计量差值|_JS0|—|_JSi|(i=1,...,N)，比较替换某一时段收益率后的差异。根据似然比检验的想法，差值越大则对拒绝原假设的贡献越大。因此，将差值中最大值对应的时段识别为发生跳跃。

步骤四，将已识别价格跳跃时段的简单和对数收益率替换为相应序列的中位数，并重复步骤一至四，直至_JS0不拒绝原假设。

步骤五，将所有发生价格跳跃时段的对数收益率累加即得当日的跳跃收益。

2.2 跳跃不平衡指标构建

在上一节中，我们简单回顾了识别股价跳跃的算法。在识别并计算出所有股票的每日的股价跳跃收益后，我们下一步就是如何将个股的跳跃行为整合成指数的跳跃指标。

参考Chordia et al(2002)和Zhang et al(2025)的做法，我们尝试构建跳跃不平衡指标^_DiNJ，如公式6所示。

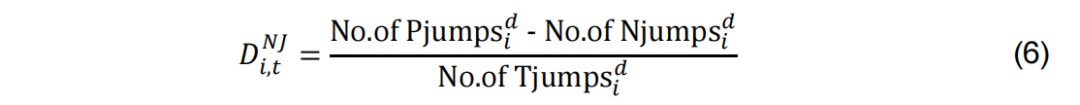
除此以外，我们还可以按照相似的逻辑构建跳跃数量不平衡指标^_JDiNJ以及跳跃幅度不平衡指标^_JRiNJ，如公式7与公式8所示。

2.3 跳跃不平衡指标初步测算

上一节中我们构建了跳跃不平衡指标，衡量了股票价格向上跳跃与向下跳跃的力量差。接下来，我们以上证指数（000001.SH）为例，来测算指标在指数择时上的效果。具体来说，我们在每个月月末，计算出每只股票的跳跃不平衡指标D、JD以及JR，然后计算指数成分股内跳跃不平衡指标的平均值，最后我们将该值与上月末的值做差分，计算出指数层面跳跃不平衡指标的变化值^{_{∆DtNJ、∆JDtNJ}}和^_∆JRtNJ。

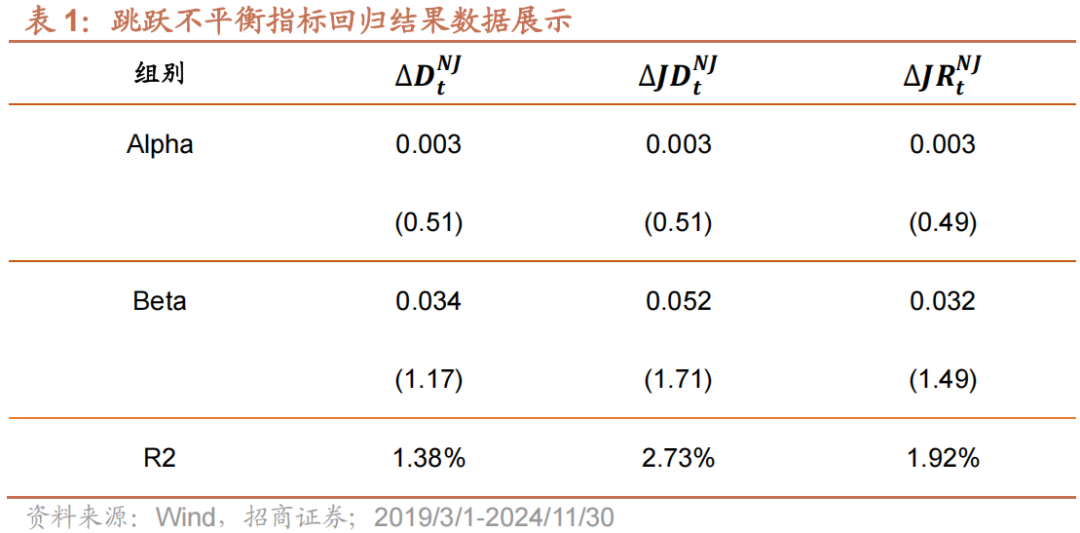
接下来，我们就来检验指标的有效性。首先，我们先用样本内回归的方式来验证指标的有效性。如式9，我们用下个月上证指数收益率_Rt+1分别与^{_{∆DtNJ、∆JDtNJ}}和^_∆JRtNJ回归。回测区间为2019年2月至2024年12月，一共71个月。

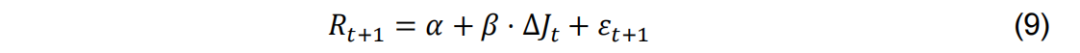
表1我们列出了回归的结果。可以看到，整体来说三个指标对指数未来收益的解释能力都不算高。对比来看，^_∆JDtNJ指标有效性相对较高，在10%显著性水平上显著。这表明当指数跳跃不平衡指标提升时，指数未来一个月上涨的概率较高。

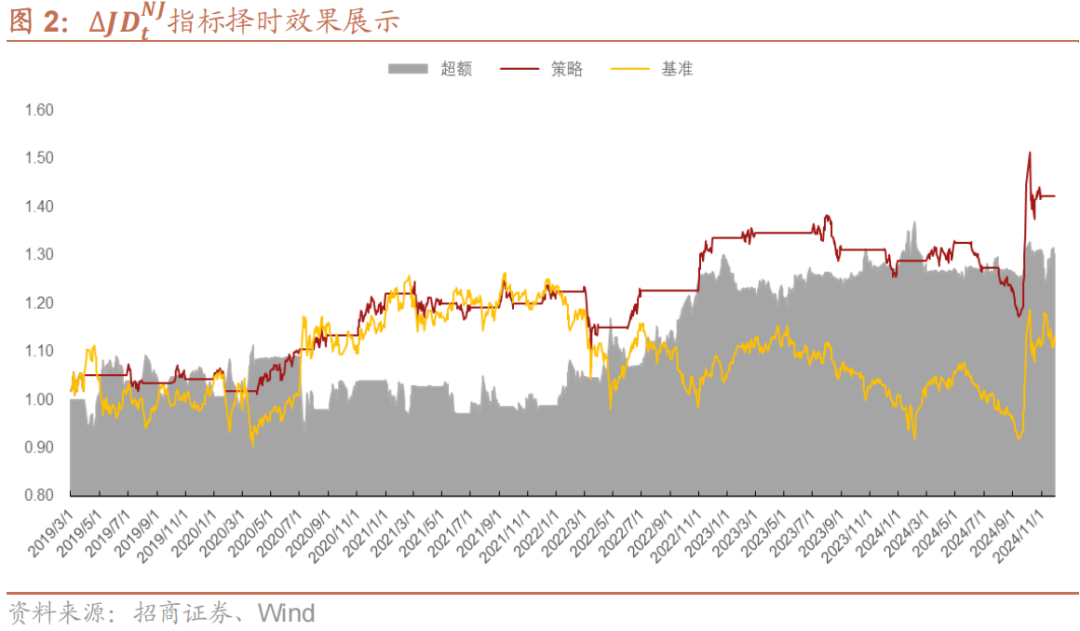
接下来，我们更直观地来测试下^_∆JDtNJ指标在指数择时上的有效性。当^_∆JDtNJ指标>0时，我们就持有上证指数，反之就空仓，策略基准为持有上证指数。回测区间为2019年3月至2024年11月，暂不考虑交易费用。

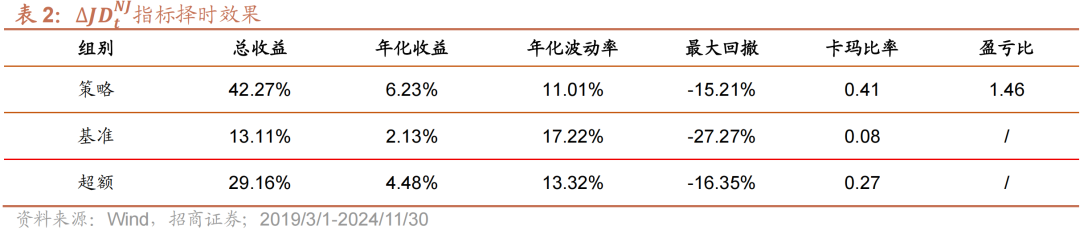
如表2与图2所示，^{_{使用∆JDtNJ指标进行择时有一定效果，但是效果整体表现不算亮眼。}}策略共开仓28次，胜率59.42%。策略年化收益6.23%，最大回撤15.21%，夏普比为0.57，卡玛比为0.41；策略超额年化收益为4.48%，夏普比为0.34，卡玛比为0.27。

III 隐含跳跃不平衡与暴露跳跃不平衡

3.1 隐含跳跃不平衡与暴露跳跃不平衡指标构建

在上一章中，我们简单回顾了股价跳跃的识别方法，基于此我们构建了指数的跳跃不平衡指标，并尝试用该指标在上证指数上进行择时，具有初步的效果。

类似于市场风险与个股的特异性风险，我们认为个股的跳跃也同样可以分为受市场跳跃影响的个股跳跃，以及不受市场跳跃影响的个股跳跃。两者的来源与其所代表的市场含义应该有所不同。

我们将受市场跳跃影响的个股跳跃称之为暴露跳跃，它反映了那些受市场跳跃影响的个股的跳跃信息。这些跳跃往往是由于整个市场的重大信息冲击引起的。这种跳跃信息更多地反映了市场参与者对市场整体波动的反应和情绪。与之对应，我们将不受市场跳跃影响的个股跳跃称之为隐含跳跃，它反映了那些不受市场跳跃影响的个股的跳跃信息。这些跳跃可能是由于个股自身的特定事件或信息冲击引起的，而不是由整个市场的跳跃所驱动，这种跳跃信息可能包含了市场参与者对个股未来表现的预期或知情交易的概率，是个股交易的“隐含信息”。

因此，我们尝试将个股的暴露跳跃不平衡指标定义^_Di,tEJ为如式10所示。

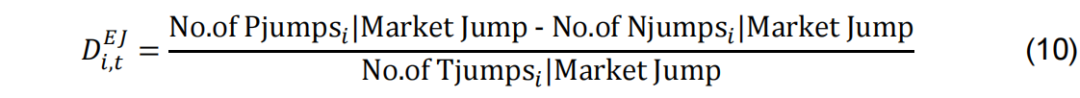
类似的，我们尝试将个股的隐含跳跃不平衡指标 ^_Di,tIJ定义为如式11所示。

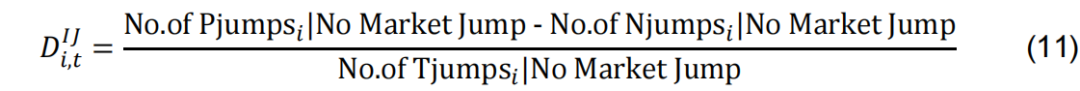
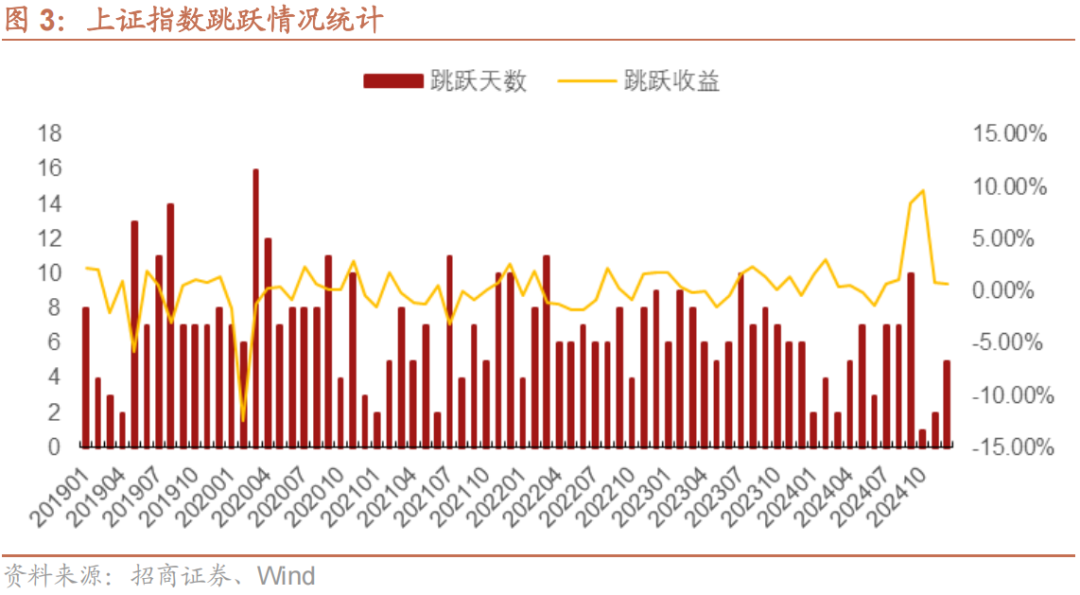
这里，我们同样以上证指数作为市场指数的代表，同样采取2.1节所采用的方法识别上证指数的股价跳跃情况。图3中我们展示了2019年以来上证指数每个月发生跳跃的天数以及总跳跃收益。上证指数每个月平均有6.8个交易日发生跳跃，平均总跳跃收益为0.33%。发生跳跃天数最多的是2020年3月，有16个交易日发生了指数的跳跃，而发生跳跃天数最少的是2024年10月，仅10月8日指数发生了跳跃。

3.2 隐含跳跃不平衡与暴露跳跃不平衡指标测算

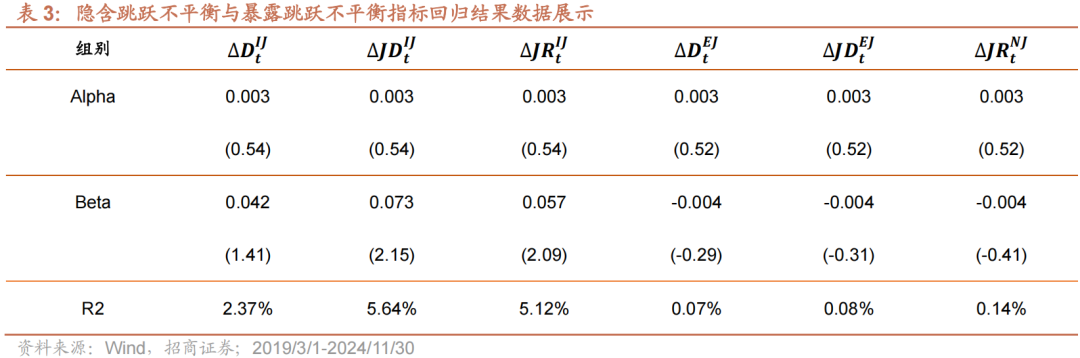
我们首先还是先以回归的方法来测算指标的有效性。表3我们列出了回归的结果。可以看到：

1） 整体来看隐含跳跃不平衡指标与未来指数收益具有正相关性，即当指数的隐含跳跃不平衡指标上升时，预期指数未来收益变大。该结果与我们预期的方向一致，由于隐含跳跃不平衡指标可能包含了市场参与者对未来表现的预期或知情交易的概率，当指标提升时，代表有更多的知情交易者看多市场，未来市场上涨的概率更高。

2） 暴露跳跃不平衡指标与未来指数收益具有负相关性，即当指数的暴露跳跃不平衡指标上升时，预期指数未来收益变小。该结果与我们预期的方向一致，由于暴露跳跃不平衡指标反映了市场参与者对市场整体波动的反应和情绪，指标提升时，代表了当前市场情绪过热，可能存在过度反应，导致短期的净卖出。

3） ^_∆JDtIJ和^_∆JRtIJ指标对指数未来收益的解释能力都较高。两个指标均在5%显著性水平上显著。这表明当指数隐含跳跃不平衡指标提升时，指数未来一个月上涨的概率较高。

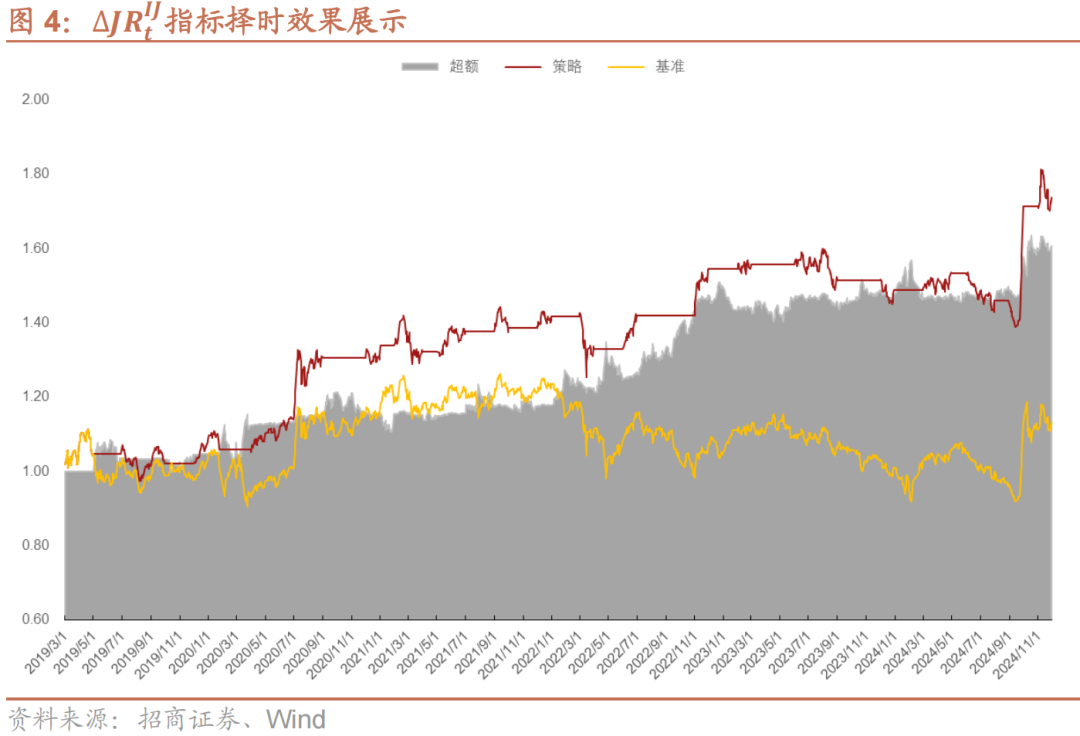
接下来，我们更直观地来测试下^_∆JRtIJ或^_∆JDtIJ指标在指数择时上的有效性。当^_∆JRtIJ或^_∆JDtIJ指标>0时，我们就持有上证指数，反之就空仓，策略基准为持有上证指数。回测区间为2019年3月至2024年11月，暂不考虑交易费用。

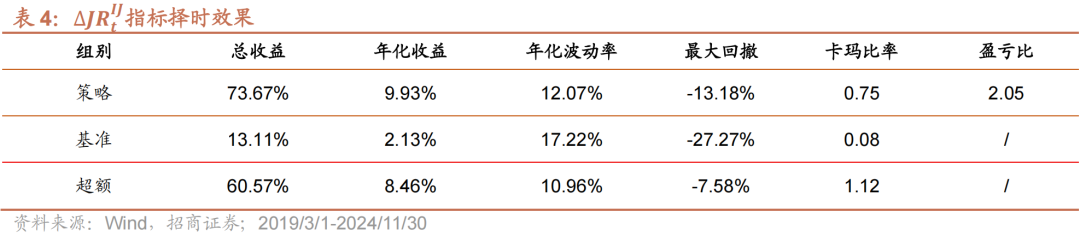
如表4与图4所示，^{_{使用∆JRtIJ进行择时具有较好的效果。}}策略共开仓33次，胜率60.87%。策略年化收益9.93%，最大回撤13.18%，夏普比为0.82，卡玛比为0.75，盈亏比达到2以上；策略超额年化收益为8.46%，夏普比为0.77，卡玛比为1.12。整体择时效果相比^_∆JDtNJ指标具有较为明显的提升。

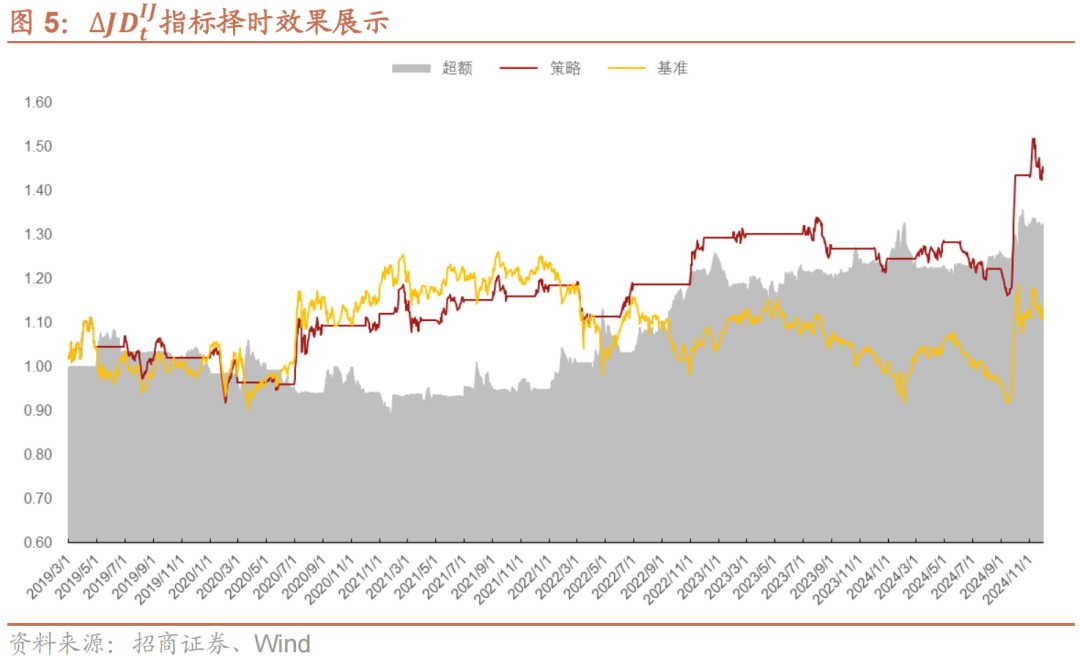
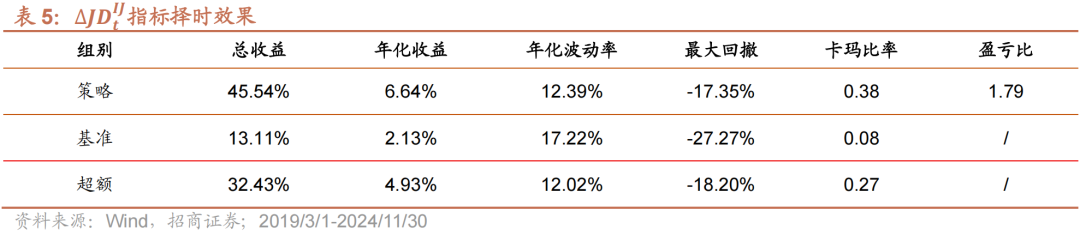
^{_{使用∆JDtIJ进行择时效果较为一般。}}策略共开仓30次，胜率56.52%。策略年化收益6.64%，夏普比为0.54，卡玛比为0.39；策略超额年化收益为4.93%，夏普比为0.41，卡玛比为0.27。

3.3 跳跃不平衡离散度指标

在前面的章节中，我们均是对个股当月的跳跃不平衡指标取平均来代表指数的跳跃不平衡指标进行择时，接下来我们也关心个股的跳跃不平衡指标的离散度是否也具有择时的效果。我们认为类似于股票Beta的离散度指标，当跳跃不平衡指标的离散度走高时，说明此时市场情绪分化程度在提高，需警惕未来情绪分化收敛，市场走弱的风险。

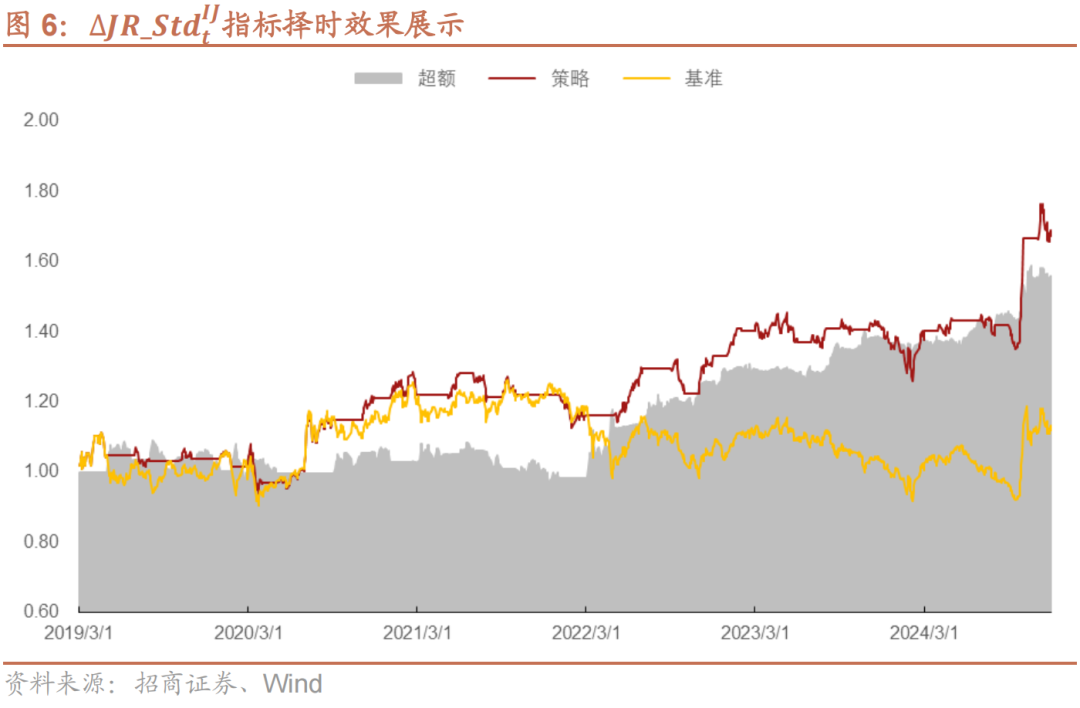
这里我们以个股当月的隐含跳跃不平衡指标取标准差来代表市场的跳跃不平衡离散度^_{JR_StdtIJ}。同样的，我们将该值与上月末的值做差分，计算出跳跃不平衡离散度^_{JR_StdtIJ}的变化值^{_{∆JR_StdtIJ}}。我们同样地来测试下^{_{∆JR_StdtIJ}}指标在指数择时上的有效性。因为我们预期跳跃平衡离散度指标与指数未来收益负相关，因此当^{_{∆JR_StdtIJ}}指标<0时，即离散度收敛时，我们就持有上证指数，反之就空仓，策略基准为持有上证指数。

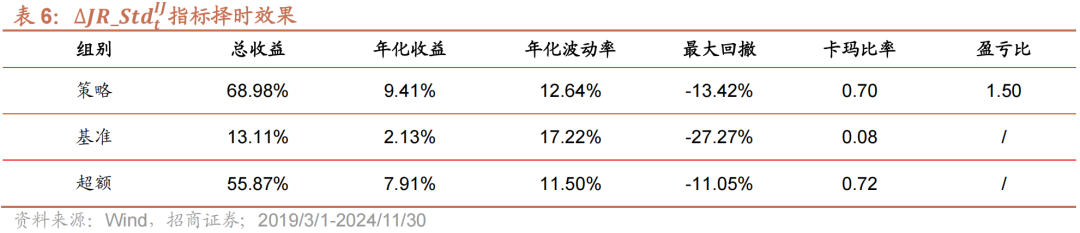
如图6与表6所示，^{_{使用∆JR_StdtIJ进行择时具有较好的效果。}}策略共开仓36次，胜率61.11%。策略年化收益9.41%，最大回撤13.42%，夏普比为0.74，卡玛比为0.7，盈亏比为1.50；策略超额年化收益为7.91%，夏普比为0.69，卡玛比为0.72。

3.4 复合指标择时

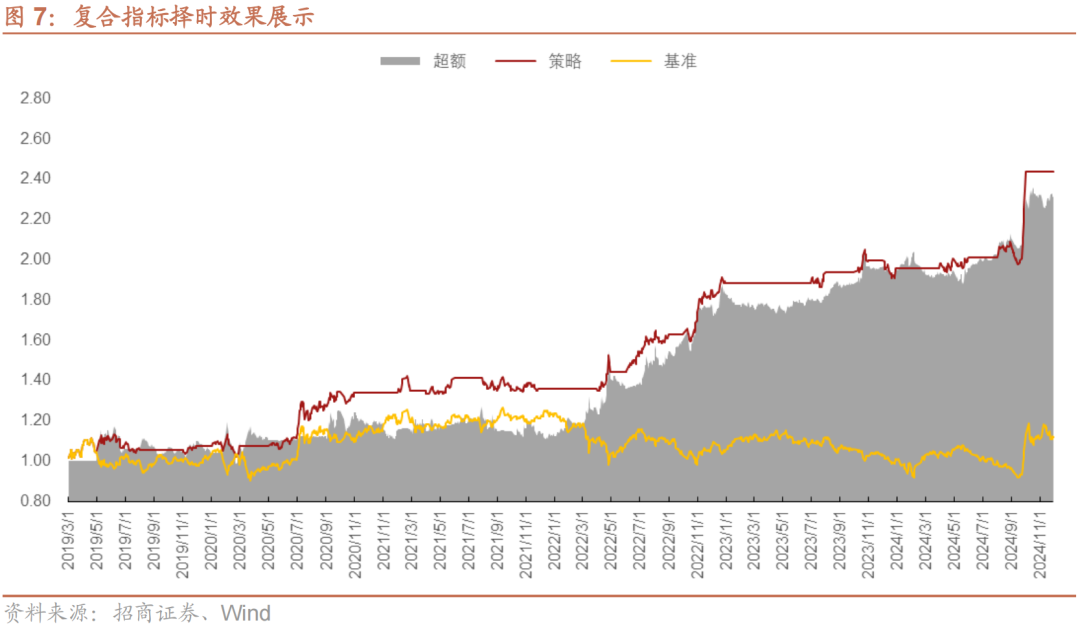
前文我们分别构建了隐含跳跃幅度不平衡指标^_JRiIJ以及跳跃不平衡离散度指标^_{JR_StdtIJ}，并验证了两个指标在指数择时上的有效性。接下来，我们尝试把两个指标进行结合，测试复合指标的择时效果。具体来说，仅有当^_∆JRtIJ>0且^{_{∆JR_StdtIJ}}<0时，即当市场隐含上涨力量变大且离散度收敛时，说明此时市场上涨的一致性力量较为充足，我们就持有上证指数；反之当^_∆JRtIJ<0且^{_{∆JR_StdtIJ}}>0时，说明此时市场隐含上涨力量变小且分歧变大，我们就做空上证指数，其他情况下就空仓，策略基准为持有上证指数。

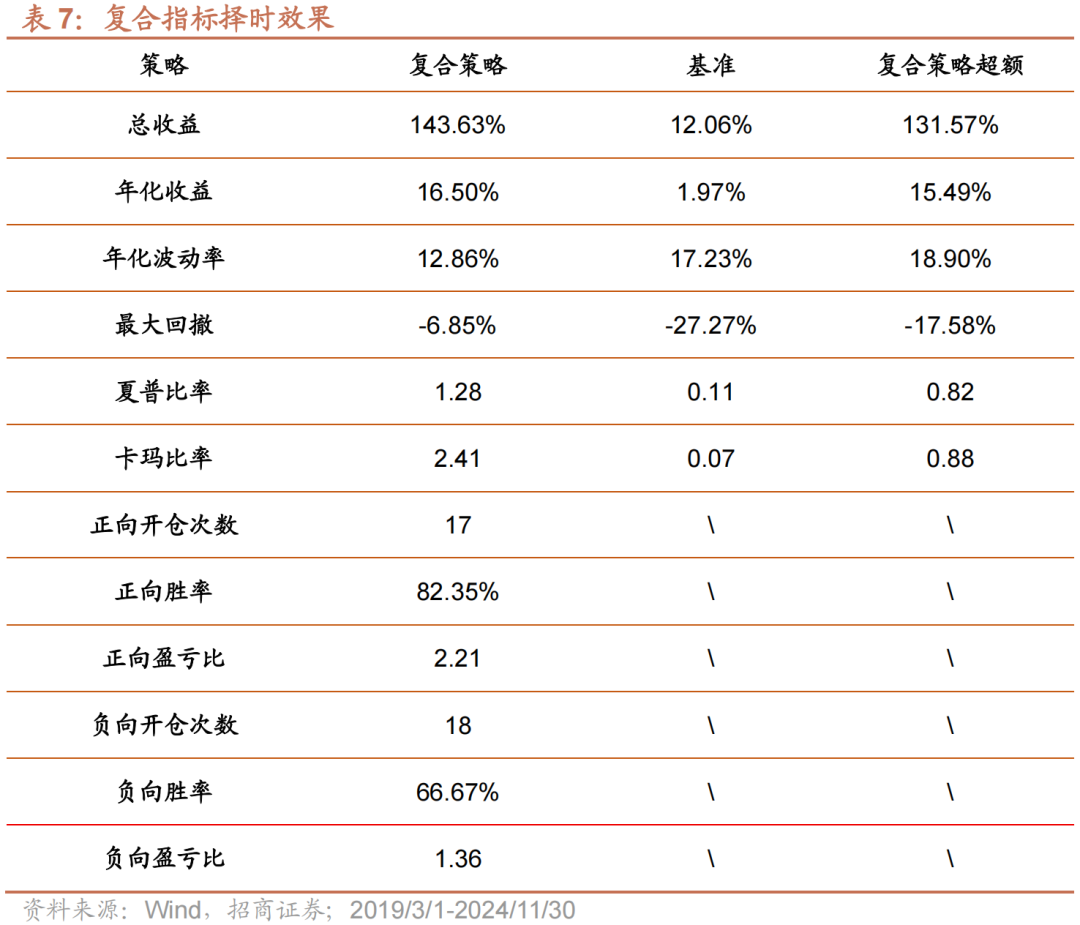
表7与图7中我们列出了复合指标择时策略的效果。复合指标择时策略年化收益为16.5%，年化超额收益15.49%，夏普比率为1.28，卡玛比率为2.41，正向开仓17次，胜率达80%以上，盈亏比2.21，负向开仓18次，胜率67%，盈亏比1.36。

IV 基于跳跃不平衡的交易策略

上文中，我们基于股价跳跃构建了隐含跳跃不平衡指标与跳跃不平衡离散度指标，并对其在上证指数中的择时效果进行了测试。在本章中，我们将进一步把策略应用在指数ETF中进行策略构建。

我们选择跟踪上证综指中规模最大的指数ETF基金，富国上证综指ETF（510210.OF）作为我们的测试对象。具体的策略为在每个月末，我们计算隐含跳跃幅度不平衡指标^_JRiIJ以及跳跃不平衡离散度指标

表9我们列出了基于跳跃不平衡的择时策略信号，对富国上证综指ETF进行择时的策略效果。策略年化收益为12.10%，夏普比率为0.89，卡玛比为1.49，策略年化超额收益9.78%，最大回撤仅为6.32%，夏普比1.14，卡玛比为1.55。整体表现较为稳健。

V 其他尝试：成长-价值风格轮动

5.1 基于股价跳跃的国证成长指数择时

前文，我们介绍了我们是如何基于股价跳跃，计算出市场的隐含跳跃强度，并根据其变化构建了择时策略。除此以外，我们发现同样的方法也适用于对成长风格走势的判断，在此基础之上，我们还构建了基于股价跳跃指标的成长-价值风格轮动策略。

同样的，首先，我们识别计算了国证成长指数（399370.SZ）的股价跳跃情况；其次，我们根据其成分股计算出每只个股的隐含跳跃收益，再做等权平均；最后，将计算出来的隐含跳跃收益均值与上个月的值计算差值，根据差值的大小判断是否持有国证成长指数。

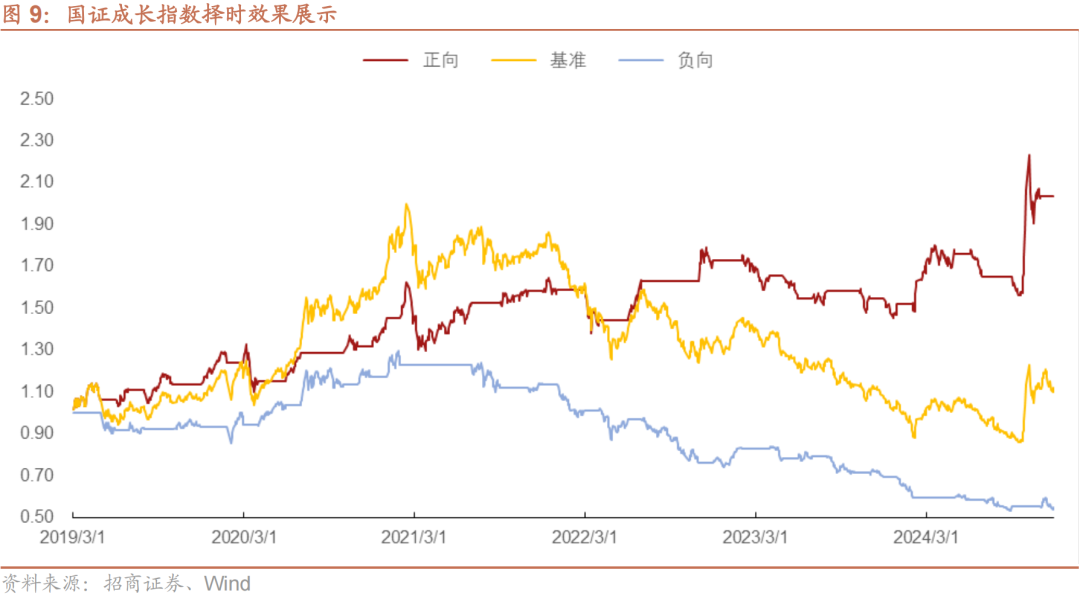
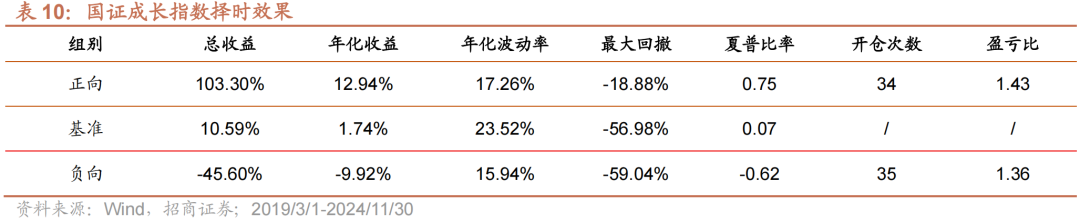
我们以^_∆JRtIJ>0持有国证成长指数作为正向策略，以^_∆JRtIJ<0持有国证成长指数作为负向策略，展示指标正负向择时的有效性。如表10与图9所示，^{_{使用∆JRtIJ对国证成长指数进行择时具有较好的效果。}}正向策略共开仓34次，胜率64.71%。策略年化收益12.94%，夏普比为0.75，卡玛比为0.69，盈亏比为1.43；负向策略共开仓35次，胜率60%，年化收益为-9.92%，盈亏比为1.36。

5.2 基于股价跳跃的成长-价值风格轮动方案

在5.1节中我们测试了基于股价跳跃的择时方法同样是适用于国证成长指数的，接下来我们在此基础上构建基于股价跳跃的成长-价值风格轮动方案。

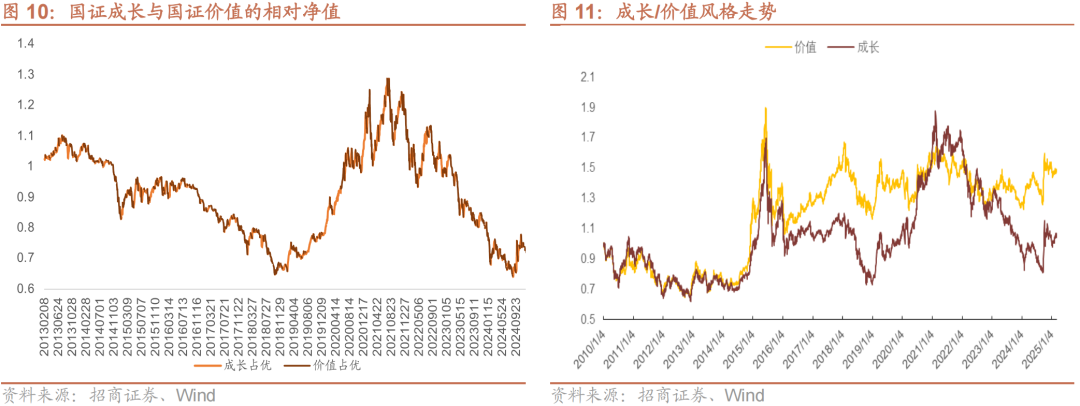
图10中我们画出了国证成长相对于国证价值指数的相对净值，可以看到可能存在某些风格阶段性占优，而其他风格则阶段性处于劣势的现象。比如，2018年-2021年成长风格相对占优，而到2021年以来价值风格相对占优。但是，我们同样也发现，从两个风格的走势来看，国证成长指数的涨跌幅相对较大，而在月度维度下两个指数同涨同跌的概率较大。经过我们的计算，仅有26%的月份两者存在涨跌不一的现象。

因此，我们认为从绝对收益的角度出发，尝试当国证成长指数隐含跳跃收益增加超过某阈值时，此时国证成长指数上涨的概率较大，持有国证成长指数，而当国证成长指数隐含跳跃收益减少超过某阈值时，说明此时整体风险较大，我们选择空仓，其他时刻则半仓持有相对较为稳健的国证价值指数。比较基准为50%的国证成长指数与50%的国证价值指数。

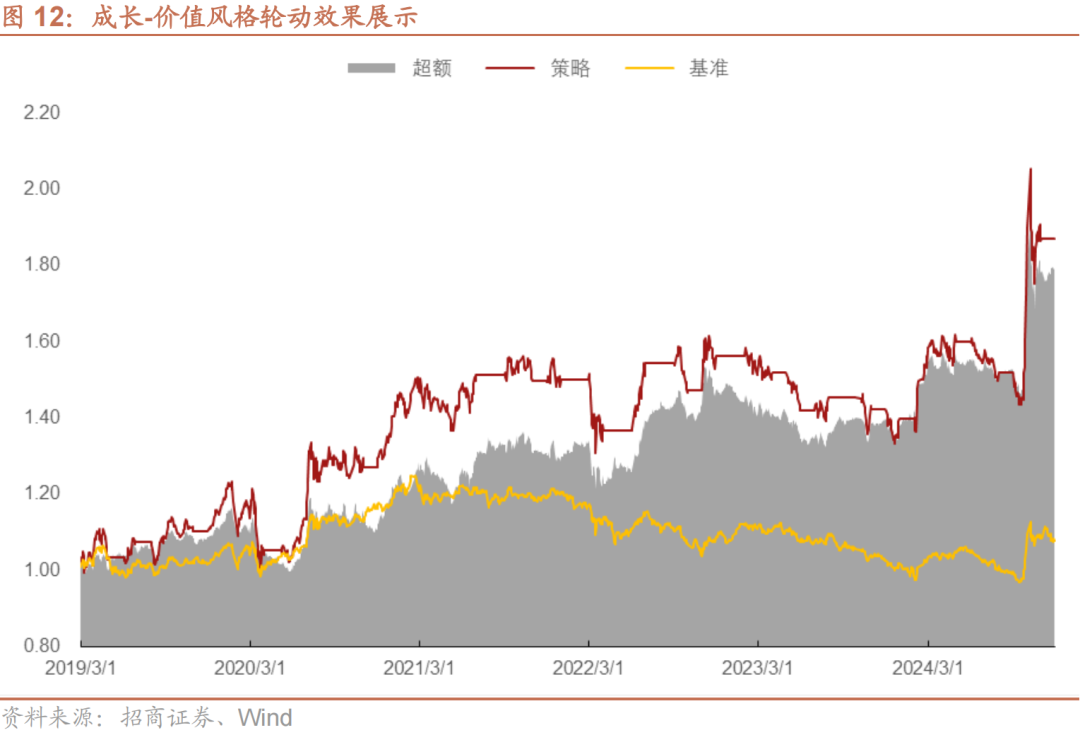
图12与表11我们展示的是选取±5%作为阈值的策略效果。策略年化收益10.95%，夏普比为0.7，卡玛比为0.75；策略超额年化收益为10.13%，夏普比为0.82，卡玛比0.82。

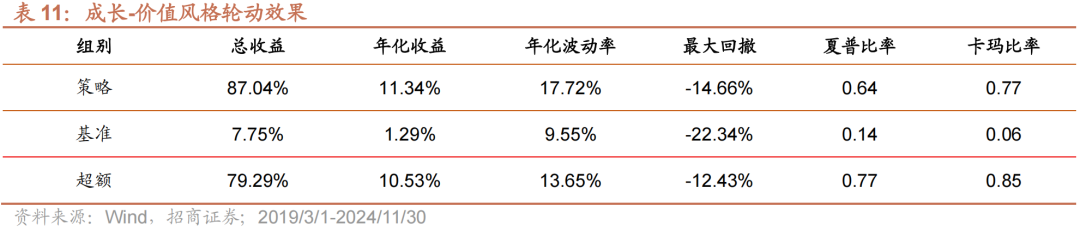
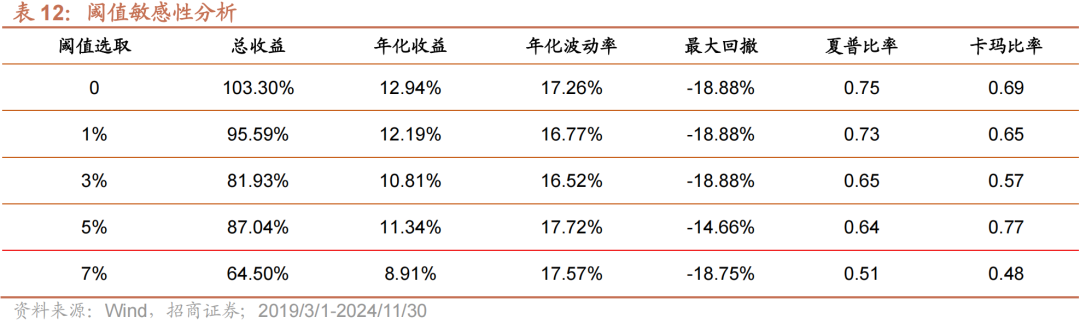
阈值选取越高，则策略中持有国证价值指数的时间区间越长，持有国证成长指数以及空仓的时间越短。表12我们展示的策略效果对于阈值参数的敏感性测试，可以看到，整体阈值的选取对策略效果的影响较不显著，策略的稳定性较好。

VI 总结

本报告研究了股价跳跃在指数择时上的应用。我们首先构建了跳跃不平衡指标，进一步创新性的将跳跃不平衡指标区分为隐含不平衡指标与暴露不平衡指标，验证了这些指标对市场收益预测的有效性。本报告的核心结论如下：

• 跳跃不平衡指标衡量了股票价格向上跳跃与向下跳跃的力量差。使用跳跃数量不平衡指标∆JDtNJ指标进行择时有一定效果。策略年化收益6.23%，夏普比为0.57，盈亏比1.46，年化超额为4.48%，夏普比为0.34。
• 我们将受市场跳跃影响的个股跳跃称之为暴露跳跃，它反映了那些受市场跳跃影响的个股的跳跃信息。这种跳跃信息更多地反映了市场参与者对市场整体波动的反应和情绪；将不受市场跳跃影响的个股跳跃称之为隐含跳跃，它反映了那些不受市场跳跃影响的个股的跳跃信息。这种跳跃信息可能包含了市场参与者对个股未来表现的预期或知情交易的概率，是个股交易的“隐含信息”。
• 使用隐含跳跃幅度不平衡指标∆JRtIJ进行择时具有较好的效果。策略共开仓33次，胜率60.87%。策略年化收益9.93%，夏普比为0.82，卡玛比为0.75，盈亏比达到2以上；年化超额为8.46%，夏普比为0.77，卡玛比为1.12。整体择时效果相比∆JDtNJ指标具有较为明显的提升。
• 我们以个股当月的隐含跳跃不平衡指标取标准差来代表市场的跳跃不平衡离散度JR_StdtIJ。将其与∆JRtIJ指标复合使用，复合指标择时策略年化收益为16.5%，年化超额收益15.49%，夏普比率为1.28，卡玛比率为2.41。
• 基于跳跃不平衡的择时策略信号，对富国上证综指ETF进行择时的策略效果整体较为稳健。策略年化收益为12.10%，夏普比率为0.89，卡玛比为1.49，策略年化超额收益9.78%，最大回撤仅为6.32%，夏普比1.14，卡玛比为1.55。
• 使用∆JRtIJ对国证成长指数进行择时同样具有较好的效果。正向策略共开仓34次，胜率64.71%。策略年化收益12.94%，夏普比为0.75，卡玛比为0.69，盈亏比为1.43；负向策略共开仓35次，胜率60%，年化收益为-9.92%，盈亏比为1.36。

*风险提示：本报告结果通过历史数据统计、建模和测算完成，在政策、市场环境发生变化时模型存在失效的风险；本报告所提及个股或基金仅表示与相关主题有一定关联性，不构成任何投资建议。

VII 参考文献

[1]. 徐龙炳, 吴文彬, 2023. 过度反应、跳跃收益与A股动量策略[J]. 中国管理科学: 1-15.

[2]. Barndorff-Nielsen O E, Shephard N, 2006. Econometrics of Testing for Jumps in Financial Economics Using Bipower Variation[J]. Journal of Financial Econometrics, 4(1): 1-30.

[3]. Jiang G J, Oomen R C A, 2008. Testing for jumps when asset prices are observed with noise–a “swap variance” approach[J]. Journal of Econometrics, 144(2): 352-370.

[4]. Jiang G J, Zhu K X, 2017. Information Shocks and Short-Term Market Underreaction[J]. Journal of Financial Economics, 124(1): 43-64.

[5]. Meng Y, Li X, Xiong X, 2024. Information shocks and short-term market overreaction: The role of investor attention[J]. International Review of Financial Analysis, 93: 103219.

[6].Zhang L，Chen Y，Liu Y K，Bouri E，2025. Jump imbalance and Chinese stock market returns