作者:大象咖啡屋
题图:大象咖啡屋微信公众号
正文
在利用金融数据,特别是高频数据(Tick数据或者LOB数据)进行预测及交易前,有以下几个主要问题需要解决。很多情况下,对于这些问题的思考反而会推翻很多固有观念,会发现它们有太多不合理的假设。
第一个问题是分布漂移。金融数据的分布漂移现象是最明显的,这也是金融时间序列预测总被视为不靠谱的重要原因之一。我觉得有两点因素:其一,金融市场是开放系统,随时都会有各种不确定性扰动,一个消息或政策就可能完全改变市场的运行状态;其二,金融交易的主体是人,被人的意识扰动的时间序列其可预测性会大大降低。
第二个问题是预测目标。很多高频预测算法简单地将未来第N个交易日的涨跌,或一个窗口期的市场平均表现作为预测目标。这类设置太过“粗暴”。以未来第N个交易日的涨跌为例,这种方式遗漏了未来N个交易日之间的所有信息,并放大了第N个交易日的随机性。
第三个问题是时间窗口。金融时间序列处理过程很难确定有效的时间窗口。传统的处理方法都是假设利用前N个(比如100)窗口长度的序列来预测后M个窗口长度的序列。这种假设显然不合理。有时预测的准确性依赖较短的序列,有时则需要观察长周期序列。如何界定有效的预测窗口也是一大难题。
上述三个问题都具有一定挑战性,窃以为只有解决了上述问题,才能开始谈金融时间序列的预测。
本篇笔记先从分布漂移问题开始探讨。
1、统计特征参数化
传统方法中,会将正态分布硬套到金融数据上,比如期权的定价过程、机器学习方法处理金融时间序列前的标准化处理过程。
不仅如此,研究者还会做出独立同分布的强假设,即某一段区间学习得到的分布统计特征,在其它区间也适用。与真实情况差得太远的话,就会拿类似肥尾效应、长尾效应来打补丁。
如果非要用(标准)正态分布来描述金融时间序列数据,那么可以将其统计特征(均值和方差)作为参数进行学习,而不是用固定值描述所有区间[1]。
上述基本思路可以采用如下公式表达:
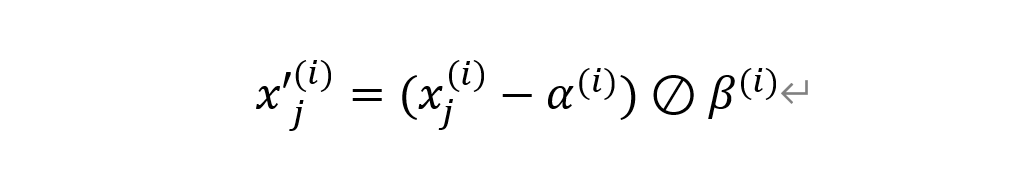
其中,x_j是原始时序数据,alpha是中心化参数(shifting, 或centering,类似求均值),beta是放缩参数(scaling,类似求方差)。上标(i)是机器学习或深度学习算法的训练轮数(epoch)。
alpha和beta是参数矩阵,可以通过神经网络等模型学习出来,示意图如下:

其中,橙色模型为标准化学习模型,它的参数就是alpha和beta(作者在[1]中还引入了过滤层(gating),放在中心化和放缩操作后,用来过滤不必要的特征)。蓝色模型为特殊任务模型,比如涨跌预测、波动率预测等,它有赖于输入序列对应的标签。
上述架构中,可以直接将未标准化的时间序列数据输入模型,其标准化学习模型的输出就是标准化后的输入数据。
这种方法有机点问题:
(1)其分布假设仍旧是正态分布,只不过对统计特征做了参数化,跟随训练数据变化。
(2)该模型的标准化结果依赖于特殊任务模型,而特殊任务模型的预测效果高度依赖于训练数据的输入与其标签。这本质上把问题推给了“预测目标”的设置。
(3)该模型没有解决窗口问题,完全依赖于特殊任务模型的设置。也就是标准化的效果取决于特殊任务模型的训练数据和相关设置。
[1] Nikolaos Passalis, etc. Deep Adaptive Input Normalization for Time Series Forecasting, 2019.
类似的工作还有[2],同样也是假设时间序列上的点服从正态分布,然后给出统计特征在训练窗口以及预测窗口都产生漂移情况下的解决方法。
[2] Wei Fan, etc. Dish-TS: A General Paradigm for Alleviating Distribution Shift in Time Series Forecasting. 2023.
2、分布差异性
我们回过头来再泛化一下分布漂移问题。给定一段金融时间序列,如下图所示,我们知道它可能在不同区间上具有不同的概率分布(如虚线分隔区间),甚至可能在每个点上。
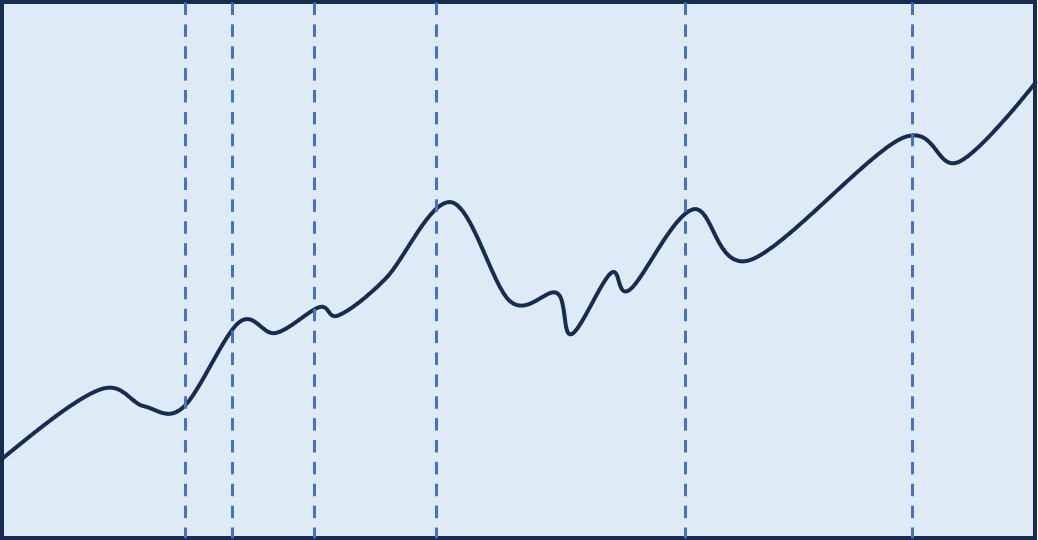
严格的做法是,我们应该将该时间序列上的每个点都看作不同的随机变量(或分布),只不过为简化计算,我们将(虚线之间)区间内的所有点都看做同一个分布。
我们不知道的是:
(1)每个时间点(或区间)是什么分布?
(2)可以切分几个不同分布的区间,区间的边界在哪里?
如果知道是什么分布,且能够比较两个分布的差异性的话,我们理论上可以通过穷举的方式找到切分的边界。
注意,这里是比较分布的差异性,而不是序列的差异性。
文章[3]使用一种类似贪心算法的方式来对原始序列按照不同分布切分为K段:首先,通过遍历数据点将原始序列分为两段,使得它们的分布差异最大;然后分别在两个子序列上进一步切分。重复上述过程,直到原始序列被切分为K段为止。
该方法有以下问题:
(1)其使用的仍旧是衡量序列相似性方法,比如余弦相似度、DTW(Dynamic time wrapping),以其近似度量分布相似性。这种方法不是太合理,因为历史数据只是原始分布的一种可能而已。
(2)分布的切分方法太过粗暴,有太多人为假设,比如首先假设原始序列包含K个分布,这显然不合理。
度量分布差异性,其实用散度更好,比如KL散度、JS散度等。所以可以考虑使用下文介绍的生成对抗网络(GAN)以及其变种来学习原始序列分布。
[3] Yuntao Du, etc. AdaRNN: Adaptive Learning and Forecasting for Time Series, 2021.
3、利用GAN学习分布
我们要学习的是金融时间序列的分布。但我们知道,手里的历史数据只是那个要学习的分布在所有可能的历史中的一种可能而已。所以,对于分布漂移研究的方法必然会受限于单个序列本身。
另外,金融时间序列中的分布漂移是一定存在的,但我们也许不必十分在意分布漂移的边界,而是尝试利用更高维的参数空间学习到整体的分布(也就是,将漂移本身也作为整体分布的基本特征)。
基于上述两个层面的思考,关于如何学习分布,一个值得尝试的模型就是GAN。下图是一个典型的GAN的模型。
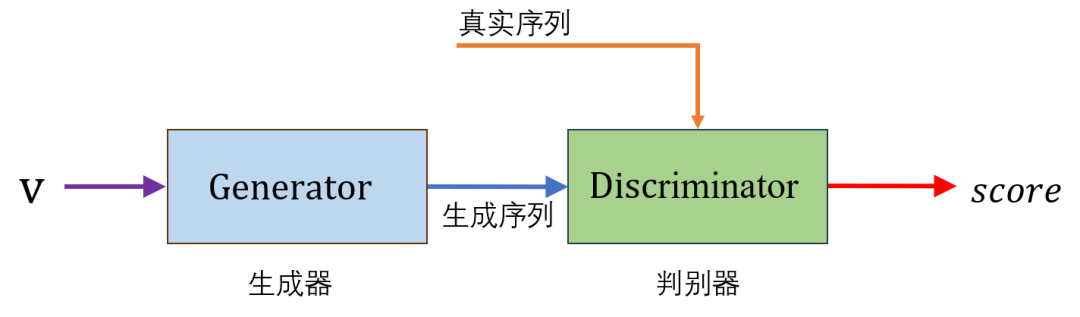
图中,生成器(Generator)用以生成时间序列。可以将生成器本身看作我们要学习得到的分布。判别器(Discriminator)将生成器生成的序列与真实序列同时作为输入,输出的评分(score),用以衡量生成序列的分布与真实序列分布的差异性。文献[4]指明了,经典的GAN中判别器所衡量的这种差异性就是JS散度。
在实际训练过程中,我们可以将原始时间序列切分成很多段,作为训练数据。然后,生成器和判别器同步迭代训练,一直到判别器所衡量的生成序列与真实序列差异性降到某个阈值以下为止。此时,我们认为生成器所生成的序列分布可以描述原始序列分布。
这种方法有几个特点:
(1)这种方式没有将分布限制在传统的分布上,比如正态分布,而是学习到了更高维的分布。
(2)但同时它将漂移问题掩盖了,而是利用这种高维的参数空间学习了整体分布。
(3)另外,学习到的生成器其实没法做序列预测,它只能给出这种分布下各种可能的序列。那么,可以利用学习到的生成器做蒙特卡洛模拟等序列生成任务。
华泰金工团队利用优化的WGAN模拟进行金融资产时间序列的生成,并表明其效果优于原始 GAN 模型[5]。
[4] Ian J. Goodfellow. Generative Adversarial Nets (2014).
[5] 华泰. WGAN 应用于金融时间序列生成(2020).
4、总结
本文将金融时间序列的分布漂移问题单独拎出来讨论了一下。
有一点我们非常明确,分布漂移问题在金融序列中是必然存在的。但是分布是如何漂移的,乃至究竟是什么分布,尚没有非常可靠的方法来解决。
也许,捕捉分布漂移在金融序列中是个伪命题。回到开篇,也许做金融序列预测本身就是个伪命题。所以是否可以尝试别的方向,利用对序列的分布建模来做其他事情呢?这是值得思考的。
版权声明:文章版权归原作者所有,部分文章由作者授权本平台发布,若有其他不妥之处的可与小编联系。
