量化实战入门—超越最小二乘法，用稳健回归让你的模型在"噪声"中捕捉真实的信号

作者：量化投资学

题图：量化投资学微信公众号

在上篇文章《ICU均线—使用稳健回归方法，突破传统均线》中，我们介绍了用重复中位数回归方法计算的ICU均线，用该均线择时取得了不错的效果。重复中位数回归是一种稳健回归的方法，本文继续对稳健回归进行探讨。在本文中，借助Python丰富的库，我们能轻而易举的实现各种稳健回归。

一、稳健回归的特点

在数据分析和统计建模中，线性回归是一种广泛应用的基础方法。但由于现实世界的数据往往并不完美，经常包含一些异常值（outliers），这些异常值可能是由于测量误差、数据录入错误或其他异常情况所导致的。在这种情况下，传统的最小二乘法（Ordinary Least Squares, OLS）可能会受到极大影响，从而导致回归结果偏差显著，甚至完全失效。这时，稳健回归（Robust Regression）便显得尤为重要。

稳健回归是一类专门设计用于应对异常值影响的回归技术，通过采用不同的估计方法和损失函数，使得回归模型对异常值的敏感性大大降低，从而提供更可靠和稳定的结果。

稳健回归的主要特点是能够有效地抵抗数据中的异常值。与最小二乘法不同，稳健回归不受单个或少量异常值的极大影响，无论数据是否存在异常值，稳健回归都能提供合理的回归结果。

参数稳健回归在量化投资中有着广泛的应用，因为金融数据通常包含噪声、异常值和非正态分布的特征。

但也要注意，稳健回归的计算成本通常高于OLS，因为它的计算过程更复杂。

二、常见的稳健回归方法及其Python实现

下面，我们借助Python的库，介绍常见的稳健回归及其实现方法。

1. 数据准备

# 在matplotlib绘图中显示中文和负号
import matplotlib.pyplot as plt
import matplotlib as mpl
mpl.rcParams['font.family'] = 'STKAITI' # 中文字体'STKAITI'
plt.rcParams['axes.unicode_minus'] = False   # 解决坐标轴负数的负号显示问题

# 关闭警告信息
import warnings
warnings.filterwarnings('ignore')

# 生成样本数据
np.random.seed(42)
X = np.linspace(0, 10, 100)
y = 2 * X + 1 + np.random.normal(0, 1, 100)
# 添加一些异常值
y[75:85] += 10

上述代码用于生成带有异常值的样本数据。

2. RLM（Robust Linear Models）回归

RLM（Robust Linear Models）回归是一类对异常值不敏感的回归方法。这些模型旨在提供比普通最小二乘法（OLS）更稳健的参数估计。RLM通过使用不同的损失函数或权重策略来减少异常值的影响。

以下是使用Python的statsmodels库实现RLM回归的示例：

# RLM（Robust Linear Models）回归
import numpy as np
import statsmodels.api as sm

# 准备数据
X = sm.add_constant(X)

# 拟合OLS和RLM模型
ols_model = sm.OLS(y, X).fit()
rlm_model = sm.RLM(y, X).fit()

# 预测
X_pred = np.linspace(0, 10, 100)
X_pred = sm.add_constant(X_pred)
y_pred_ols = ols_model.predict(X_pred)
y_pred_rlm = rlm_model.predict(X_pred)

# 绘制结果

plt.scatter(X[:, 1], y, color='blue', alpha=0.5, label='数据点')
plt.plot(X_pred[:, 1], y_pred_ols, color='red', label='OLS回归线')
plt.plot(X_pred[:, 1], y_pred_rlm, color='green', label='RLM回归线')
plt.legend()
plt.title('OLS vs RLM回归')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()

回归结果如下：

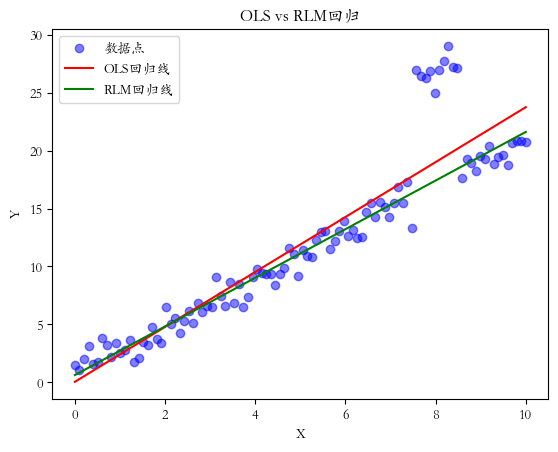
这个例子展示了如何使用RLM回归来拟合一个包含异常值的数据集，并与OLS回归进行比较。可以看到RLM回归在处理含有异常值或离群点的数据时特别有用，因为它可以提供比OLS更可靠的参数估计。

3. Quantile 回归

Quantile回归（分位数回归）是一种用于估计因变量的条件分位数的回归方法。与普通最小二乘回归估计条件均值不同，Quantile回归可以估计条件分布的任何分位数，使其特别适用于处理异方差性或非对称分布的数据。

Quantile回归在分位数取0.5时称为中位数回归，中位数回归提供了一个"典型"或"中心"趋势的估计。中位数回归在处理存在异常值或高度偏斜的数据时特别有用，因为它不像普通最小二乘法那样容易受到极端值的影响。

以下是使用Python的statsmodels库实现Quantile回归的示例：

# Quantile 回归

import numpy as np
import statsmodels.api as sm

# 准备数据
X = sm.add_constant(X)

# 拟合不同分位数的回归模型
quantiles = [0.1, 0.5, 0.9]
models = [sm.QuantReg(y, X).fit(q=q) for q in quantiles]

# 绘制结果
plt.scatter(X[:, 1], y, color='blue', alpha=0.5, label='数据点')

for i, q in enumerate(quantiles):
    y_pred = models[i].predict(X)
    plt.plot(X[:, 1], y_pred, label=f'{q}分位数回归线')

plt.legend()
plt.title('Quantile回归')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()

回归结果如下：

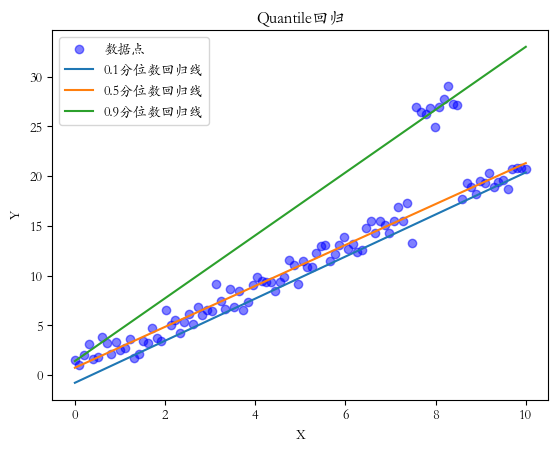
在这个例子中，我们拟合了0.1、0.5（中位数）和0.9分位数的回归线。我们可以观察X如何影响y分布的不同部分。例如，0.9分位数回归线显示了y的高值是如何随X变化的，而0.1分位数回归线显示了y的低值是如何随X变化的。我们可以看到，0.5中位数回归对异常值具有鲁棒性，因为中位数不受极端值的影响。

4. Theil-Sen 回归

Theil-Sen回归是一种稳健的线性回归方法,对异常值不敏感。它通过计算所有数据点对的斜率的中位数来估计回归线的斜率。

以下是使用Python的scikit-learn库实现Theil-Sen回归的示例:

import numpy as np
from sklearn.linear_model import TheilSenRegressor

# 创建并拟合Theil-Sen回归器
theil_sen = TheilSenRegressor(random_state=42)
theil_sen.fit(X.reshape(-1, 1), y)

# 预测
y_pred = theil_sen.predict(X.reshape(-1, 1))

# 绘制结果
plt.scatter(X, y, color='blue', label='数据点')
plt.plot(X, y_pred, color='red', label='Theil-Sen回归线')
plt.legend()
plt.title('Theil-Sen回归')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()

回归结果如下：

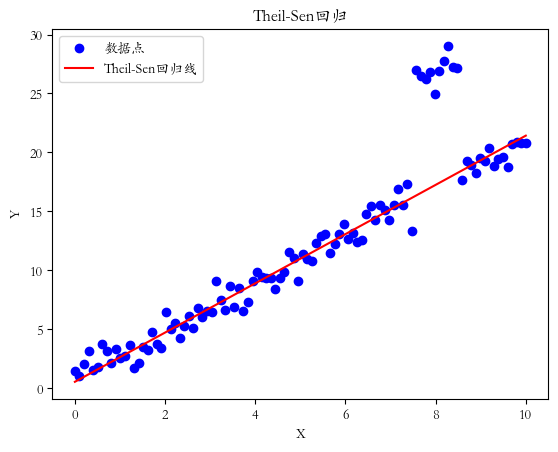
5. RANSAC 回归

RANSAC（Random Sample Consensus，随机抽样一致）回归是一种迭代方法，用于从包含大量异常值的数据集中估计模型参数。它特别适用于存在许多离群点的数据。

以下是使用Python的scikit-learn库实现RANSAC回归的示例：

# RANSAC 回归

import numpy as np
from sklearn.linear_model import RANSACRegressor

# 创建并拟合RANSAC回归器
ransac = RANSACRegressor()
ransac.fit(X.reshape(-1, 1), y)

# 预测
inlier_mask = ransac.inlier_mask_
outlier_mask = np.logical_not(inlier_mask)
line_X = np.arange(X.min(), X.max())[:, np.newaxis]
line_y_ransac = ransac.predict(line_X)

# 绘制结果
plt.scatter(X, y, color='blue', label='数据点')
plt.plot(line_X, line_y_ransac, color='red', linewidth=2,label='RANSAC 回归线')
plt.legend()
plt.xlabel("X")
plt.ylabel("Y")
plt.title('RANSAC回归')
plt.show()

回归结果如下：

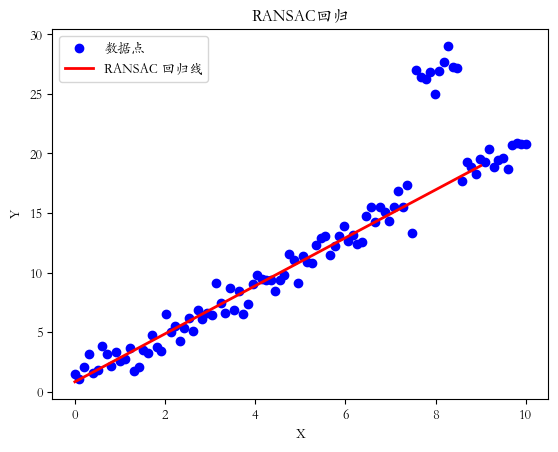
6. Huber 回归

Huber回归是一种结合了最小二乘回归和绝对值回归优点的方法，对异常值具有一定的鲁棒性。它使用一个称为Huber损失的函数，该函数在残差较小时类似于平方损失，在残差较大时类似于绝对值损失。这种方法在处理含有异常值的数据时比普通最小二乘法更稳健，但又不像中位数回归那样完全忽视异常值的信息。

以下是使用Python的scikit-learn库实现Huber回归的示例：

# Huber 回归

import numpy as np
from sklearn.linear_model import HuberRegressor

# 创建并拟合Huber回归器
huber = HuberRegressor()
huber.fit(X.reshape(-1, 1), y)

# 预测
y_pred = huber.predict(X.reshape(-1, 1))

# 绘制结果
plt.scatter(X, y, color='blue', label='数据点')
plt.plot(X, y_pred, color='red', label='Huber回归线')
plt.legend()
plt.title('Huber回归')
plt.xlabel('X')
plt.ylabel('Y')
plt.show()

回归结果如下：

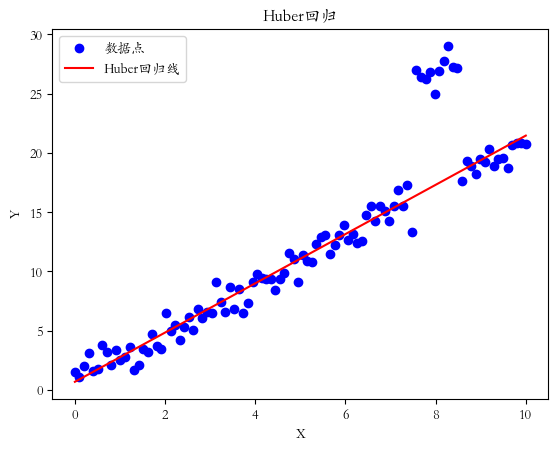
本文探讨了多种稳健回归的方法，这些技术不仅能够应对异常值和非标准分布的挑战，还能在复杂的实际数据中揭示更可靠的关系。稳健回归方法并非是对传统最小二乘法的简单替代，而是数据分析工具箱中的强大补充。它们为我们提供了更全面的视角，使我们能够在数据的"噪声"中捕捉到真实的信号。通过合理使用稳健回归方法，量化投资策略可以在面对金融市场的不确定性和异常性时，获得更稳定、可靠的结果。

版权声明：文章版权归原作者所有，部分文章由作者授权本平台发布，若有其他不妥之处的可与小编联系。